विषय
एक ठोस के पार्श्व क्षेत्र को उसके सभी पार्श्व चेहरों के संयुक्त क्षेत्र के रूप में परिभाषित किया गया है। पार्श्व चेहरे आधार और शीर्ष को छोड़कर ठोस के पक्ष हैं। एक पंचकोणीय पिरामिड के लिए, पार्श्व क्षेत्र पिरामिड के पांच त्रिकोणीय पक्षों का संयुक्त क्षेत्र है। इसकी गणना करने के लिए, आपको त्रिकोणीय पक्षों के क्षेत्रों को खोजना होगा और उन्हें एक साथ जोड़ना होगा।
एक त्रिभुज का क्षेत्र
पंचकोणीय पिरामिड के प्रत्येक भाग में एक त्रिभुज होता है। इसलिए, पक्षों में से एक का क्षेत्र त्रिकोण की ऊंचाई के आधार के आधे हिस्से के बराबर है। जब आप पंचकोणीय पिरामिड के प्रत्येक त्रिकोणीय पक्षों के क्षेत्र को जोड़ते हैं, तो आपको पिरामिड का कुल पार्श्व क्षेत्र मिलेगा।
अपना समीकरण सेट करें
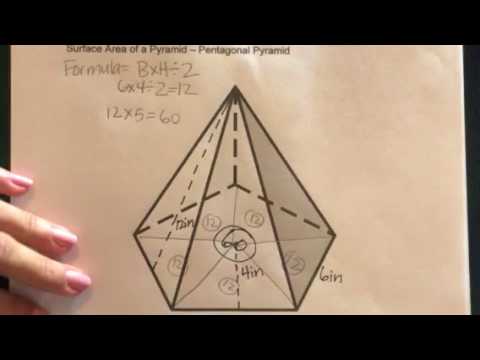
पिरामिड के प्रत्येक त्रिभुज की ऊँचाई को तिरछी ऊँचाई के रूप में जाना जाता है। एक तरफ की तिरछी ऊँचाई पिरामिड के शीर्ष से आधार के दोनों पक्षों के मध्य बिंदु की दूरी है। इसलिए, पंचकोणीय पिरामिड के पार्श्व क्षेत्र के लिए सूत्र 1/2 x आधार एक x तिरछा ऊँचाई एक + 1/2 x आधार दो x तिरछी ऊँचाई दो + 1/2 x आधार तीन x तिरछी ऊँचाई तीन + 1/2 x है आधार चार x तिरछा ऊँचाई चार + १/२ x आधार पाँच x तिरछा ऊँचाई पाँच। यदि पंचकोणीय पिरामिड के सभी त्रिकोणीय चेहरे समान हैं, तो इस सूत्र को 5/2 x आधार x तिरछी ऊँचाई पर सरलीकृत किया जा सकता है। क्योंकि सभी आधार पेंटागन की परिधि को बराबर करने के लिए गठबंधन करते हैं, आप सूत्र को पेंटागन x तिरछी ऊंचाई के 1/2 x परिधि के रूप में दर्शा सकते हैं।
तिरछी ऊँचाई का पता लगाना
यदि आपको पिरामिड की तिरछी ऊंचाई नहीं दी जाती है, तो आपको ठोस के भीतर मौजूद विभिन्न त्रिकोणों पर विचार करके इसे खोजना होगा। उदाहरण के लिए, एक सही पंचकोणीय पिरामिड में, पिरामिड का शीर्ष इसके आधार के केंद्र के ऊपर है। यह पेंटागन के केंद्र और उसके किनारों के मध्य बिंदु के बीच एक आधार के साथ एक सही त्रिकोण बनाता है, पेंटागन के केंद्र और पिरामिड के शीर्ष के बीच की ऊंचाई और तिरछी ऊंचाई के बराबर एक कर्ण है। इस व्यवस्था के कारण, आप तिरछी ऊँचाई निर्धारित करने के लिए पायथागॉरियन प्रमेय का उपयोग कर सकते हैं।
नियमित बनाम। अनियमित पिरामिड
यदि पेंटागोनल पिरामिड का आधार एक नियमित पेंटागन है, तो इसका मतलब है कि आधार के सभी पक्ष समान हैं, जैसा कि पक्षों के बीच के कोण हैं। यदि पिरामिड का आधार नियमित पेंटागन नहीं है, तो इसके प्रत्येक त्रिकोणीय चेहरे अलग हो सकते हैं। पिरामिड के शीर्ष के स्थान के आधार पर, इसका मतलब यह हो सकता है कि प्रत्येक त्रिकोण क्षेत्र अलग है। इस स्थिति में, सूत्र 5/2 x आधार x तिरछी ऊँचाई तक सरल नहीं हो सकता है। इसके बजाय, आपको प्रत्येक पक्ष के क्षेत्र को जोड़ना होगा।