विषय
- टीएल; डीआर (बहुत लंबा; डिडंट रीड)
- स्क्वायर रूट फ़ंक्शंस
- स्क्वायर रूट फ़ंक्शंस के डोमेन
- स्क्वायर रूट फ़ंक्शंस की रेंज
गणित में, एक फ़ंक्शन का डोमेन आपको बताता है कि फ़ंक्शन के कौन से मान मान्य हैं। इसका मतलब यह है कि उस डोमेन के भीतर कोई भी मान फ़ंक्शन में काम करेगा, जबकि डोमेन के बाहर आने वाला कोई भी मूल्य नहीं होगा। कुछ फ़ंक्शंस (जैसे रैखिक फ़ंक्शंस) में ऐसे डोमेन होते हैं जिनमें x के सभी संभावित मान शामिल होते हैं। अन्य (जैसे समीकरण जहां x हर के भीतर प्रकट होता है) शून्य से विभाजित होने से बचने के लिए x के कुछ मानों को बाहर करते हैं। स्क्वायर रूट फ़ंक्शंस में कुछ अन्य फ़ंक्शंस की तुलना में अधिक प्रतिबंधित डोमेन हैं, क्योंकि वर्गाकार रूट (रेडिकैंड के रूप में जाना जाता है) के भीतर मान एक सकारात्मक संख्या होनी चाहिए।
टीएल; डीआर (बहुत लंबा; डिडंट रीड)
एक वर्गमूल फ़ंक्शन का डोमेन x के सभी मान हैं, जिसके परिणामस्वरूप एक रेडिकैंड होता है जो शून्य के बराबर या उससे अधिक होता है।
स्क्वायर रूट फ़ंक्शंस
एक स्क्वायर रूट फ़ंक्शन एक फ़ंक्शन होता है जिसमें एक कट्टरपंथी होता है, जिसे आमतौर पर स्क्वायर रूट कहा जाता है। यदि आप यह सुनिश्चित करते हैं कि यह कैसा दिखता है, तो f (x) = consideredx को एक मूल वर्गमूल फ़ंक्शन माना जाता है। इस स्थिति में, x एक सकारात्मक संख्या नहीं हो सकती है; सभी रेडिकल शून्य के बराबर या उससे अधिक होने चाहिए, या वे एक अपरिमेय संख्या उत्पन्न करते हैं।
इसका मतलब यह नहीं है कि सभी वर्ग मूल कार्य एक संख्या के वर्गमूल के समान सरल हैं। अधिक जटिल वर्गमूल कार्यों में कट्टरपंथी के भीतर गणना हो सकती है, गणना जो कट्टरपंथी परिणाम को संशोधित करती है या यहां तक कि एक बड़े फ़ंक्शन के हिस्से के रूप में एक कट्टरपंथी (जैसे कि अंश में प्रदर्शित होने या किसी समीकरण के हर में)। इन अधिक जटिल कार्यों के उदाहरण f (x) = 2 x (x + 3) या g (x) = --x - 4 जैसे दिखते हैं।
स्क्वायर रूट फ़ंक्शंस के डोमेन
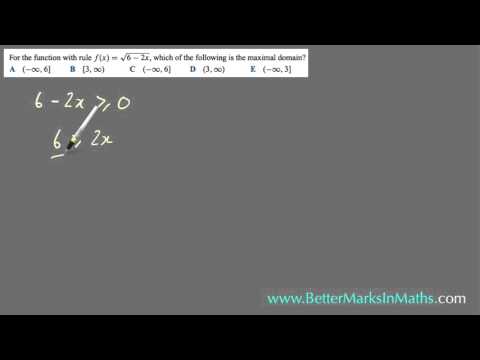
एक वर्गमूल फ़ंक्शन के डोमेन की गणना करने के लिए, असमानता x x 0 को x को रेडिकैंड द्वारा प्रतिस्थापित x से हल करें। ऊपर दिए गए उदाहरणों में से एक का उपयोग करके, आप विषमता में x के बराबर त्रिज्या (x + 3) सेट करके f (x) = 2 x (x + 3) का डोमेन पा सकते हैं। इससे आपको x + 3 which 0 की असमानता मिलती है, जिसे आप दोनों पक्षों द्वारा 3 घटाकर हल कर सकते हैं। यह आपको x, -3 का एक समाधान देता है, जिसका अर्थ है कि आपका डोमेन x के मान से अधिक या बराबर है। आप इसे [-3, also) के रूप में भी लिख सकते हैं, बाईं ओर ब्रैकेट के साथ यह दर्शाता है कि -3 एक विशिष्ट सीमा है जबकि दाईं ओर कोष्ठक दिखाता है कि as नहीं है। चूंकि रेडिकैंड नकारात्मक नहीं हो सकता है, इसलिए आपको केवल सकारात्मक या शून्य मानों की गणना करनी होगी।
स्क्वायर रूट फ़ंक्शंस की रेंज
किसी फ़ंक्शन के डोमेन से संबंधित एक अवधारणा इसकी सीमा है। जबकि एक फ़ंक्शन डोमेन x के सभी मान हैं जो फ़ंक्शन के भीतर मान्य हैं, इसकी सीमा y के सभी मानों में है जिसमें फ़ंक्शन मान्य है। इसका मतलब है कि किसी फ़ंक्शन की श्रेणी उस फ़ंक्शन के सभी मान्य आउटपुट के बराबर होती है। आप इसे फ़ंक्शन के बराबर y सेट करके गणना कर सकते हैं, और फिर किसी भी मान को खोजने के लिए हल कर सकते हैं जो मान्य नहीं हैं।
वर्गाकार रूट फ़ंक्शंस के लिए, इसका अर्थ है कि फ़ंक्शन की श्रेणी सभी मानों का उत्पादन करती है जब x एक रेडिकैंड में परिणाम होता है जो शून्य के बराबर या उससे अधिक होता है। अपने वर्गमूल फ़ंक्शन के डोमेन की गणना करें, और फिर रेंज निर्धारित करने के लिए फ़ंक्शन में अपने डोमेन के मूल्य का इनपुट करें। यदि आपका कार्य f (x) = √ (x - 2) है और आप डोमेन की गणना x के सभी मानों से अधिक या 2 के बराबर करते हैं, तो आपके द्वारा y = √ (x - 2) में डाला गया कोई भी मान्य मूल्य आपको दे देगा एक परिणाम जो शून्य से अधिक या उसके बराबर है।इसलिए आपकी सीमा y or 0 या [0, ≥) है।