
विषय
ज्यामिति में, एक अष्टकोण एक बहुभुज होता है जिसमें आठ भुजाएँ होती हैं। एक नियमित अष्टकोण में आठ समान पक्ष और समान कोण होते हैं। नियमित अष्टकोण को आमतौर पर स्टॉप संकेतों से पहचाना जाता है। ऑक्टाहेड्रोन एक आठ-पक्षीय पॉलीहेड्रॉन है। एक नियमित ऑक्टाहेड्रोन में समान लंबाई के किनारों के साथ आठ त्रिकोण होते हैं। यह प्रभावी रूप से दो वर्ग पिरामिड उनके ठिकानों पर बैठक है।
अष्टकोना क्षेत्र सूत्र
लंबाई के किनारों के साथ एक नियमित अष्टकोना के क्षेत्र के लिए सूत्र "ए" 2 (1 + sqrt (2)) a ^ 2 है, जहां "sqrt" वर्गमूल को इंगित करता है।
व्युत्पत्ति
एक अष्टकोण को 4 आयतों, केंद्र में एक वर्ग और कोनों में चार समद्विबाहु त्रिभुज के रूप में देखा जा सकता है।
वर्ग क्षेत्र ए ^ 2 का है।
त्रिकोण में पाइथागोरस प्रमेय द्वारा पक्ष, ए / वर्गर्ट (2) और / वर्गमीटर (2) हैं। इसलिए, प्रत्येक का क्षेत्रफल ^ 2/4 है।
आयतें क्षेत्र के हैं * a / sqrt (2)।
इन 9 क्षेत्रों का योग 2a ^ 2 (1 + sqrt (2)) है।
ऑक्टाहेड्रोन वॉल्यूम फॉर्मूला
पक्षों के एक नियमित ऑक्टाहेड्रन की मात्रा के लिए सूत्र "ए" एक ^ 3 * sqrt (2) / 3 है।
व्युत्पत्ति
चार-तरफा पिरामिड का क्षेत्रफल आधार * ऊंचाई / 3. का क्षेत्र है। एक नियमित अष्टकोना का क्षेत्र इसलिए 2 * आधार * ऊंचाई / 3 है।
आधार = ^ ^ 2 तुच्छ रूप से।
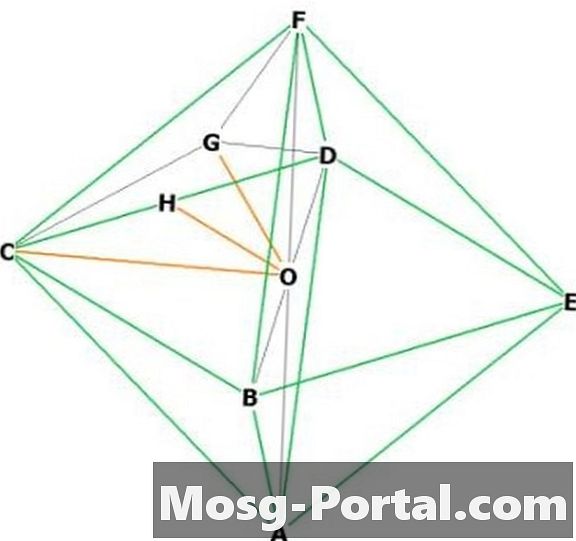
दो आसन्न कोने चुनें, "F" और "C" कहें "O" केंद्र में है। FOC एक समद्विबाहु समकोण त्रिभुज है जिसका आधार "," है, इसलिए OC और पाइथागोरस प्रमेय द्वारा लंबाई / a / sqrt (2) है। इतनी ऊँचाई = a / sqrt (2)।
तो एक नियमित ऑक्टाहेड्रोन की मात्रा 2 * (^ 2) * / a sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3 है।
सतह क्षेत्र
नियमित ऑक्टाहेड्रोन की सतह पक्ष के एक समबाहु त्रिभुज का क्षेत्र है "ए" 8 बार का चेहरा।
पाइथागोरस प्रमेय का उपयोग करने के लिए, शीर्ष से आधार तक एक रेखा छोड़ें। यह दो सही त्रिकोण बनाता है, लंबाई के कर्ण के साथ "ए" और एक तरफ की लंबाई "ए / 2।" इसलिए, तीसरा पक्ष sqrt = sqrt (3) a / 2 होना चाहिए। तो एक समबाहु त्रिभुज का क्षेत्रफल ऊंचाई है * आधार / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4।
8 पक्षों के साथ, एक नियमित ऑक्टाहेड्रोन का सतह क्षेत्र 2 * sqrt (3) * a ^ 2 है।