विषय
- समानांतर सर्किट आरेख
- टिप्स
- समानांतर सर्किट उदाहरण
- समानांतर बनाम श्रृंखला सर्किट
- श्रृंखला-समानांतर सर्किट
विद्युत सर्किट में उनके सर्किट तत्व श्रृंखला या समानांतर में व्यवस्थित हो सकते हैं। श्रृंखला सर्किट में, तत्व एक ही शाखा का उपयोग करके जुड़े होते हैं जो उनमें से प्रत्येक के माध्यम से विद्युत प्रवाह को एक-एक करके। समानांतर सर्किट में, तत्वों की अपनी अलग शाखाएं होती हैं। इन सर्किटों में, करंट पूरे रास्ते अलग-अलग ले सकता है।
क्योंकि समांतर परिपथ में करंट अलग-अलग पथ ले सकता है, समांतर परिपथ में करंट आइस स्थिर रहता है। इसके बजाय, उन शाखाओं के लिए जो एक दूसरे के समानांतर जुड़े हुए हैं, प्रत्येक शाखा में वोल्टेज या संभावित गिरावट स्थिर है। इसका कारण यह है कि वर्तमान प्रत्येक शाखा में स्वयं को प्रत्येक मात्रा में वितरित करता है जो प्रत्येक शाखा के प्रतिरोध के विपरीत आनुपातिक हैं। यह वर्तमान को सबसे बड़ा बनाता है जहां प्रतिरोध सबसे कम है और इसके विपरीत।
इन गुणों को समानांतर सर्किट दो या दो से अधिक रास्तों से प्रवाहित करने की अनुमति देते हैं, जिससे यह स्थिर और कुशल प्रणाली के माध्यम से घरों और बिजली के उपकरणों में एक मानक उम्मीदवार बन जाता है। यह एक सर्किट के अन्य हिस्सों के माध्यम से बिजली का प्रवाह देता है जब एक हिस्सा क्षतिग्रस्त या टूट जाता है, और वे अलग-अलग इमारतों में समान रूप से बिजली वितरित कर सकते हैं। इन विशेषताओं को एक आरेख और एक समानांतर सर्किट के उदाहरण के माध्यम से प्रदर्शित किया जा सकता है।
समानांतर सर्किट आरेख
टिप्स
समानांतर सर्किट उदाहरण
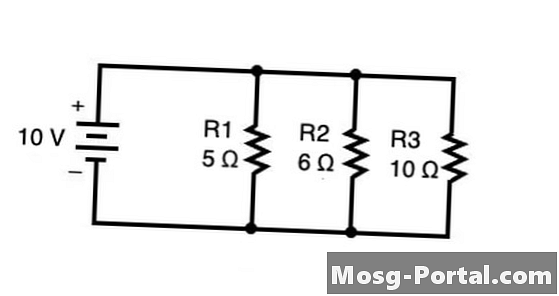
एक दूसरे के साथ समानांतर में व्यवस्थित प्रतिरोधों के कुल प्रतिरोध को खोजने के लिए, सूत्र का उपयोग करें 1 / आरसंपूर्ण = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / आरएन जिसमें प्रत्येक प्रतिरोधक के प्रतिरोध को समीकरण के दाईं ओर सम्मिलित किया जाता है। उपरोक्त आरेख में, ओम (be) में कुल प्रतिरोध की गणना निम्नानुसार की जा सकती है:
ध्यान दें कि आप समीकरण के दोनों किनारों को चरण 3 से चरण 4 तक केवल "फ्लिप" कर सकते हैं जब समीकरण के दोनों किनारों पर केवल एक ही शब्द होता है (इस मामले में, 1 / आरसंपूर्ण बाईं ओर और 14/30 Ω दायीं तरफ)।
आपके द्वारा प्रतिरोध की गणना करने के बाद, वर्तमान और वोल्टेज की गणना ओम कानून का उपयोग करके की जा सकती है वी = आई / आर जिसमें वी वोल्टेज वोल्ट में मापा जाता है, मैं वर्तमान को amps में मापा जाता है, और आर ओम में प्रतिरोध है। समानांतर सर्किट में, प्रत्येक पथ के माध्यम से धाराओं का योग स्रोत से कुल वर्तमान है। सर्किट में प्रत्येक रोकनेवाला पर वर्तमान को रोकनेवाला के लिए वोल्टेज बार प्रतिरोध को गुणा करके गणना की जा सकती है। वोल्टेज पूरे सर्किट में स्थिर रहता है इसलिए वोल्टेज बैटरी या वोल्टेज स्रोत का वोल्टेज है।
समानांतर बनाम श्रृंखला सर्किट
••• सैयद हुसैन अतहरसीरीज़ सर्किट में, करंट निरंतर होता है, वोल्टेज ड्रॉप प्रत्येक रेसिस्टर के प्रतिरोध पर निर्भर करता है और कुल रेजिस्टेंस प्रत्येक व्यक्तिगत रेसिस्टर का योग होता है। समानांतर सर्किट में, वोल्टेज निरंतर होता है, करंट प्रत्येक रेसिस्टर पर निर्भर करता है और कुल प्रतिरोध का व्युत्क्रम प्रत्येक व्यक्तिगत रेसिस्टर के व्युत्क्रम का योग होता है।
कैपेसिटर और इंडिकेटर्स का उपयोग समय के साथ श्रृंखला और समानांतर सर्किट में चार्ज को बदलने के लिए किया जा सकता है। एक श्रृंखला सर्किट में, कुल समाई सर्किट का (चर द्वारा दिया गया) सी), समय के साथ चार्ज करने के लिए एक संधारित्र की क्षमता, प्रत्येक व्यक्तिगत कैपेसिटर्स के व्युत्क्रम का व्युत्क्रम योग है, और कुल अधिष्ठापन (मैं), समय के साथ प्रभार देने के लिए प्रेरकों की शक्ति, प्रत्येक प्रारंभ करनेवाला का योग है। इसके विपरीत, एक समानांतर सर्किट में, कुल समाई प्रत्येक व्यक्ति संधारित्र का योग है, और कुल अधिष्ठापन का व्युत्क्रम प्रत्येक व्यक्तिगत अधिष्ठापन के व्युत्क्रम का योग है।
श्रृंखला और समानांतर सर्किट में भी अलग-अलग कार्य होते हैं। एक श्रृंखला सर्किट में, यदि एक हिस्सा टूट गया है, तो वर्तमान में सर्किट के माध्यम से प्रवाह नहीं होगा। समानांतर सर्किट में, एक व्यक्तिगत शाखा का उद्घाटन उस शाखा में केवल वर्तमान को रोकता है। शेष शाखाएँ काम करना जारी रखेंगी क्योंकि करंट के पास कई रास्ते होते हैं जो सर्किट के पार ले जा सकते हैं।
श्रृंखला-समानांतर सर्किट

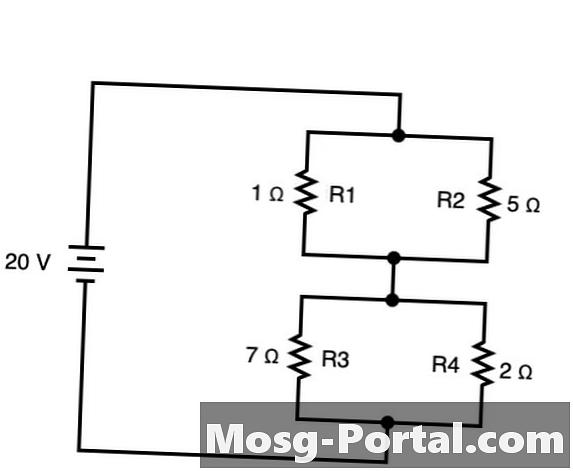
ऐसे सर्किट जिनमें दोनों शाखाओं वाले तत्व होते हैं, जो इस तरह से जुड़े होते हैं कि उन शाखाओं के बीच एक दिशा में वर्तमान प्रवाह होता है दोनों श्रृंखला और समानांतर। इन मामलों में, आप सर्किट के लिए उपयुक्त श्रृंखला और समानांतर दोनों से नियम लागू कर सकते हैं। उपरोक्त उदाहरण में, आर 1 तथा आर 2 एक दूसरे के साथ समानांतर रूप में हैं R5, और इसलिए हैं R3 तथा R4 बनाने के लिए R6। उन्हें समानांतर रूप से संक्षेप में प्रस्तुत किया जा सकता है:
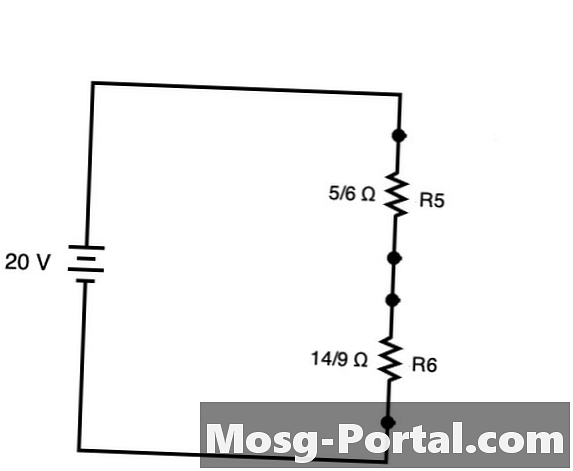
सीधे ऊपर दिखाए गए सर्किट को बनाने के लिए सर्किट को सरल बनाया जा सकता है R5 तथा R6। इन दो प्रतिरोधों को सीधा जोड़ा जा सकता है जैसे कि सर्किट श्रृंखला थी।
आरसंपूर्ण = 5/6 14 + 14/9 / = 45/54 84 + 84/54 Ω = 129/54 18 = 43/18 Ω या लगभग 2.38 Ω
20 के साथ वी वोल्टेज के रूप में, ओम कानून यह दर्शाता है कि कुल वर्तमान बराबर है वी / आर, या 20 वी / (43/18 /) = 360/43 ए या के बारे में 8.37 ए। इस कुल धारा के साथ, आप ओम कानून का उपयोग करके आर 5 और आर 6 दोनों में वोल्टेज ड्रॉप निर्धारित कर सकते हैं (वी = मैं / आर) भी।
के लिये R5, V5 = 360/43 ए x 5/6 1800 = 1800/258 वी या के बारे में 6.98 वी।
के लिये R6, V6 = 360/43 ए x 14/9 16 = 1680/129 वी या के बारे में 13.02 वी।
अंत में, ये वोल्टेज के लिए गिरता है R5 तथा R6 वर्तमान की गणना करने के लिए मूल समानांतर सर्किट में वापस विभाजित किया जा सकता है आर 1 तथा आर 2 के लिये R5 तथा आर 2 तथा R3 के लिये R6 ओम कानून का उपयोग करना।
I1 = (1800/258 वी) / 1 / = 1800/258 ए या abou_t 6.98 A._
I2 = (1800/258 वी) / 5 Ω = 1500/43 ए या abou_t 34.88 A._
I3 = (680/129 वी) / 7 60 = 4760/129 ए या के बारे में 36.90 ए.
I3 = (680/129 वी) / 2 60 = 1360/129 ए या के बारे में 10.54 ए।