एक समभुज त्रिभुज के क्षेत्रफल की गणना कैसे करें

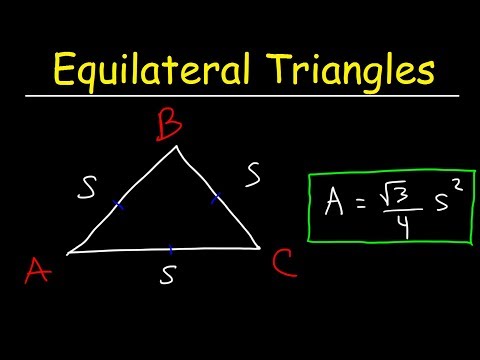
एक समबाहु त्रिभुज एक त्रिभुज है जिसमें तीनों समान लंबाई के होते हैं। एक त्रिभुज जैसे दो आयामी बहुभुज का सतह क्षेत्र कुल क्षेत्रफल बहुभुज के पक्षों द्वारा समाहित है। यूक्लिडीय ज्यामिति में एक समबाहु त्रिभुज के तीन कोण भी बराबर माप के होते हैं। चूंकि यूक्लिडियन त्रिकोण के कोणों का कुल माप 180 डिग्री है, इसका मतलब है कि एक समभुज त्रिकोण के कोण सभी 60 डिग्री मापते हैं। एक समबाहु त्रिभुज के क्षेत्रफल की गणना तब की जा सकती है, जब इसके किनारों की लंबाई ज्ञात हो।

आधार और ऊंचाई ज्ञात होने पर एक त्रिभुज का क्षेत्रफल ज्ञात करें। आधार एस और ऊंचाई एच के साथ किसी भी दो समान त्रिकोण लें। हम हमेशा इन दो त्रिभुजों के साथ आधार s और ऊंचाई h का समांतर चतुर्भुज बना सकते हैं। चूँकि एक समांतर चतुर्भुज का क्षेत्रफल s x h है, इसलिए एक त्रिभुज का क्षेत्रफल इसलिए x s x h है।



लाइन सेगमेंट एच के साथ दो समकोण त्रिभुज में समबाहु त्रिभुज का निर्माण करें। इनमें से एक दाएं त्रिकोण लंबाई s के कर्ण, एक के पैर की लंबाई h और दूसरे पैर की लंबाई s / 2 है।

S के संदर्भ में व्यक्त करें। चरण 2 में गठित सही त्रिभुज का उपयोग करना, हम जानते हैं कि पायथागॉरियन सूत्र द्वारा s ^ 2 = (s / 2) ^ 2 + h ^ 2 है। इसलिए, h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, और हमारे पास अब h = (3 ^ 1/2) s है / 2।

चरण 1 में प्राप्त त्रिभुज क्षेत्र के सूत्र में चरण 3 में प्राप्त h के मान को प्रतिस्थापित करें। A = h sxh और h = (3 ^ 1/2) s / 2 के बाद से, अब हमारे पास A = (s (3 ^) है 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4।




चरण 4 में प्राप्त एक समभुज त्रिभुज के क्षेत्रफल के सूत्र का उपयोग करें। समबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के लिए लंबाई के किनारे 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2) ) (2 ^ 2) / 4 = (3 ^ 1/2)।