विषय
त्रिभुज के तीसरे पक्ष का माप खोजना जब आप अन्य दो पक्षों के माप को जानते हैं केवल तभी काम करता है जब आपके पास एक सही त्रिकोण या कम से कम एक अन्य कोण का माप हो। इस जानकारी के बिना आपके पास तीसरे पक्ष की लंबाई का पता लगाने के लिए पर्याप्त डेटा नहीं है। एक समकोण त्रिभुज को तीसरे कोण में बनाया गया है, क्योंकि कोण में से एक 90 डिग्री का होना चाहिए।
पायथागॉरियन प्रमेय का उपयोग करते हुए सही त्रिकोण
त्रिभुज को अपने पेपर पर समकोण, या पैर, "a" और "b" से सटे दोनों पक्षों पर लेबल बनाएं, कर्ण या तीसरे पक्ष को लेबल करें "c।"
अपना समीकरण सेट करें ताकि ए2 + बी2 = सी2। यह पायथागॉरियन प्रमेय है जिसका उपयोग अज्ञात पक्ष के समाधान के लिए किया जाता है।
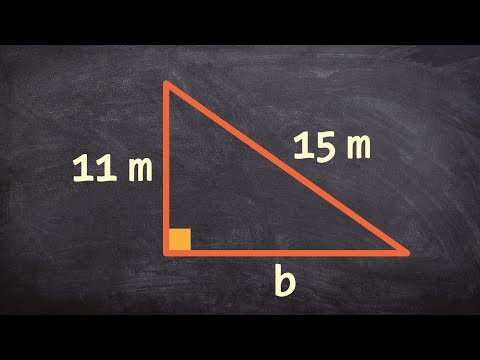
समीकरण में आपके द्वारा ज्ञात लंबाई को भरें। कर्ण हमेशा एक सही त्रिकोण में सबसे लंबा पक्ष होता है। यह आपके काम की जाँच करने का एक शानदार तरीका है, क्योंकि यदि दोनों में से कोई भी कर्ण से अधिक लंबा नहीं है, तो आप जानते हैं कि आपने एक त्रुटि की है।
अज्ञात पक्ष के लिए हल करें। यदि आप कर्ण के लिए हल कर रहे हैं, तो आप दोनों संख्याओं को "वर्ग" और "बी" भरें, और फिर संख्याओं को एक साथ जोड़ें। अपने उत्तर तक पहुंचने के लिए परिणामी राशि का वर्गमूल प्राप्त करने के लिए अपने कैलकुलेटर का उपयोग करें। यदि आप एक के पैर के लिए हल कर रहे हैं, तो आपको दूसरे पैर को "सी" के रूप में उसी तरफ ले जाने की आवश्यकता है, जिसे घटाकर। यह शेष पैर को अकेला छोड़ देता है, जिससे आप इसके लिए हल कर सकते हैं। इसका मतलब है कि आप "सी" संख्या और ज्ञात पैर को वर्गाकार करते हैं। चुकता सी मान से चुकता पैर मान घटाएँ। परिणामी संख्या का वर्गमूल प्राप्त करें और आपके पास अज्ञात पैर के लिए अपना उत्तर है।
सीन्स के कानून का उपयोग करना
त्रिभुज को सेट करें ताकि कोण के विपरीत पक्ष कोण के साथ मेल खाता हो। कोण ए के विपरीत पक्ष को ए के रूप में लेबल करें, कोण बी के पार के पक्ष को बी के रूप में और पक्ष को कोण सी के विपरीत।
एक / sinA = b / sinB = c / sinC पढ़ने के लिए समीकरण लिखिए। यह आपको अपने अज्ञात पक्ष के समाधान के लिए मूल बातें देता है।
उस कोण को लें जिसे आप जानते हैं और उस कोण की साइन को निर्धारित करने के लिए कैलकुलेटर का उपयोग करें। अधिकांश वैज्ञानिक कैलकुलेटर आपने कोण संख्या में दर्ज किए हैं और फिर "पाप" लेबल वाला बटन दबाएं।
उस कोण के पाप के मूल्य द्वारा कोण से जुड़े पक्ष की लंबाई को विभाजित करें। यह आपको एक संख्या देता है जिसे आमतौर पर एक सन्निकटन के रूप में लिखा जाता है, क्योंकि दशमलव स्थान अनिश्चित काल के लिए बंद हो जाते हैं। इस उदाहरण के उद्देश्य से इस नए नंबर X को कॉल करें।
दूसरे ज्ञात पक्ष का मान लें और इसे X से विभाजित करें। यह नया नंबर नए कोण के साइन के बराबर है।
कैलकुलेटर में संख्या दर्ज करें और कोण में डिग्री प्राप्त करने के लिए "पाप -1" को हिट करें। अब आप अज्ञात पक्ष के कोण के लिए हल कर सकते हैं।
दो ज्ञात कोणों को एक साथ जोड़ें और कुल को 180 से घटाएं। एक त्रिभुज के अंदर सभी कोणों को 180 डिग्री तक जोड़ना होगा।
नए कोण की साइन की गणना कैलकुलेटर में दर्ज करके और "पाप" बटन दबाकर करें। एक्स द्वारा उत्तर को गुणा करें और यह आपको अज्ञात पक्ष की लंबाई देता है।
पाइथागोरस प्रमेय के साथ-साथ एक नई विधि का उपयोग करते हुए एक उदाहरण के लिए, विधि का उपयोग कर कोसाइन का उपयोग करते हुए, वीडियो देखें:
सुझाव: सीन्स के कानून को कहा गया है या सभी जानकारी को सम्मिलित करके काम किया जा सकता है ताकि कोण की साइन को पक्ष की लंबाई से विभाजित किया जा सके।
चेतावनी: समस्या को देखने के लिए कि आप क्या गुणा कर रहे हैं और विभाजित कर रहे हैं ताकि आप यह समझ सकें कि समस्या कैसे काम कर रही है। याद रखें, आप समीकरण के दोनों किनारों पर समान कार्य करना चाहिए ताकि पक्षों को बराबर रखा जा सके।