पेंडुलम मोशन के नियम

विषय

• टीएल; डीआर (बहुत लंबा; डिडंट रीड)
• सरल आवर्त गति
• एक साधारण पेंडुलम के नियम
• सरल पेंडुलम व्युत्पत्ति
• पेंडुलम आंदोलन को प्रभावित करने वाले कारक
• पेंडुलम उदाहरण की लंबाई
• सरल पेंडुलम परिभाषा
• पेंडुलम में न्यूटन के नियम

पेंडुलम में दिलचस्प गुण हैं जो भौतिक विज्ञानी अन्य वस्तुओं का वर्णन करने के लिए उपयोग करते हैं। उदाहरण के लिए, ग्रह की कक्षा एक समान पैटर्न का अनुसरण करती है और स्विंग सेट पर झूलते हुए पेंडुलम पर youre की तरह महसूस हो सकता है। ये गुण कानूनों की एक श्रृंखला से आते हैं जो पेंडुलम के आंदोलन को नियंत्रित करते हैं। इन कानूनों को सीखने से, आप भौतिकी के कुछ बुनियादी सिद्धांतों और सामान्य रूप से गति को समझना शुरू कर सकते हैं।

टीएल; डीआर (बहुत लंबा; डिडंट रीड)

एक पेंडुलम की गति का उपयोग करके वर्णन किया जा सकता है = (t) = =_{अधिकतम}cos (2πt / T) जिसमें θ केंद्र के नीचे स्ट्रिंग और ऊर्ध्वाधर रेखा के बीच के कोण का प्रतिनिधित्व करता है, टी समय का प्रतिनिधित्व करता है, और टी वह अवधि है, जो पेंडुलम गति के एक पूर्ण चक्र के घटित होने के लिए आवश्यक है (द्वारा मापा गया) 1 / च), एक पेंडुलम के लिए गति की।

सरल आवर्त गति

सरल आवर्त गति, या गति जो बताती है कि कैसे एक वस्तु संतुलन संतुलन से विस्थापन की मात्रा के अनुपात में दोलन करता है, का उपयोग एक पेंडुलम के समीकरण का वर्णन करने के लिए किया जा सकता है। एक पेंडुलम बॉब स्विंग को इस बल द्वारा गति में रखा जाता है क्योंकि यह आगे और पीछे चलता है।

••• सैयद हुसैन अतहर

पेंडुलम आंदोलन को संचालित करने वाले कानूनों ने एक महत्वपूर्ण संपत्ति की खोज की। भौतिकविदों ने एक ऊर्ध्वाधर और एक क्षैतिज घटक में बलों को तोड़ दिया। पेंडुलम गति में, तीन बल सीधे पेंडुलम पर काम करते हैं: बॉब का द्रव्यमान, गुरुत्वाकर्षण और स्ट्रिंग में तनाव। द्रव्यमान और गुरुत्वाकर्षण दोनों लंबवत काम करते हैं। चूंकि पेंडुलम ऊपर या नीचे नहीं जाता है, इसलिए स्ट्रिंग तनाव का ऊर्ध्वाधर घटक द्रव्यमान और गुरुत्वाकर्षण को रद्द कर देता है।

इससे पता चलता है कि एक पेंडुलम के द्रव्यमान की गति के लिए कोई प्रासंगिकता नहीं है, लेकिन क्षैतिज स्ट्रिंग तनाव करता है। सरल हार्मोनिक गति परिपत्र गति के समान है। आप एक वृत्ताकार पथ में घूमती हुई वस्तु का वर्णन कर सकते हैं जैसा कि ऊपर की आकृति में दिखाया गया है और इसके समान वृत्ताकार पथ में त्रिज्या का निर्धारण करता है। फिर, सर्कल सेंटर, ऑब्जेक्ट्स स्थिति, और दोनों दिशाओं x और y में विस्थापन के बीच सही त्रिकोण के त्रिकोणमिति का उपयोग करके आप समीकरण पा सकते हैं x = rsin (() तथा y = rcos (θ)।

सरल हार्मोनिक गति में किसी वस्तु का एक आयामी समीकरण किसके द्वारा दिया जाता है x = r cos (ωt)। आप आगे स्थानापन्न कर सकते हैं ए के लिये आर जिसमें ए है आयामवस्तुओं से अधिकतम विस्थापन प्रारंभिक स्थिति।

कोणीय वेग ω समय के संबंध में टी इन कोणों के लिए θ द्वारा दिया गया है ω = ωt। यदि आप आवृत्ति के लिए कोणीय वेग से संबंधित समीकरण को प्रतिस्थापित करते हैं च, ω = 2πf_, आप इस परिपत्र गति की कल्पना कर सकते हैं, फिर, आगे और पीछे झूलते हुए एक पेंडुलम के हिस्से के रूप में, फिर परिणामी सरल हार्मोनिक गति समीकरण _x = A cos ((2πfटी)।

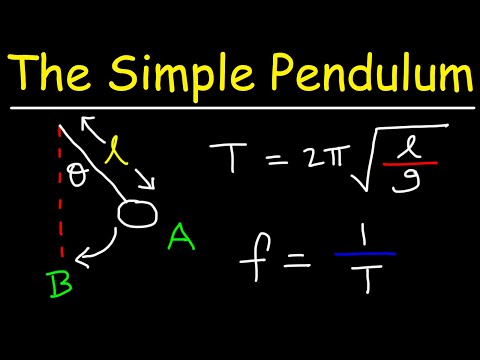
एक साधारण पेंडुलम के नियम

••• सैयद हुसैन अतहर

स्प्रिंग पर द्रव्यमान की तरह पेंडुलम इसके उदाहरण हैं सरल हार्मोनिक दोलक: एक पुनर्स्थापना बल होता है जो इस बात पर निर्भर करता है कि पेंडुलम कितना विस्थापित है, और उनकी गति का उपयोग करके वर्णन किया जा सकता है सरल हार्मोनिक थरथरानवाला समीकरण = (t) = =_{अधिकतम}cos (2πt / T) जिसमें θ केंद्र के नीचे स्ट्रिंग और ऊर्ध्वाधर रेखा के बीच के कोण का प्रतिनिधित्व करता है, टी समय का प्रतिनिधित्व करता है और टी है अवधिपेंडुलम गति के एक पूर्ण चक्र के होने के लिए आवश्यक समय (द्वारा मापा गया) 1 / च), एक पेंडुलम के लिए गति की।

θ_{अधिकतम} पेंडुलम गति के दौरान अधिकतम कोण को परिभाषित करने का एक और तरीका है और पेंडुलम आयाम को परिभाषित करने का एक और तरीका है। यह चरण "सरल पेंडुलम परिभाषा" अनुभाग के तहत नीचे समझाया गया है।

एक साधारण पेंडुलम के नियमों का एक और निहितार्थ यह है कि निरंतर लंबाई के साथ दोलन की अवधि स्ट्रिंग के अंत में वस्तु के आकार, आकार, द्रव्यमान और सामग्री से स्वतंत्र होती है। यह सरल पेंडुलम व्युत्पत्ति और परिणाम के समीकरणों के माध्यम से स्पष्ट रूप से दिखाया गया है।

सरल पेंडुलम व्युत्पत्ति

आप एक के लिए समीकरण निर्धारित कर सकते हैं साधारण पेंडुलमएक पेंडुलम के लिए गति के समीकरण के साथ शुरुआत चरणों की एक श्रृंखला से एक सरल हार्मोनिक थरथरानवाला पर निर्भर करता है कि परिभाषा। चूँकि एक पेंडुलम के गुरुत्वाकर्षण का बल पेंडुलम आंदोलन के बल के बराबर होता है, आप न्यूटन के दूसरे नियम का एक पेंडुलम द्रव्यमान का उपयोग करके उन्हें एक दूसरे के बराबर सेट कर सकते हैं म, स्ट्रिंग लंबाई एल, कोण θ, गुरुत्वाकर्षण त्वरण जी और समय अंतराल टी.

••• सैयद हुसैन अतहर

आप न्यूटन के दूसरे नियम को जड़ता के क्षण के बराबर सेट करते हैं मैं = श्री²_ कुछ मास के लिए _m और परिपत्र गति की त्रिज्या (इस मामले में स्ट्रिंग की लंबाई) आर कोणीय त्वरण का समय α.

एक साधारण पेंडुलम व्युत्पत्ति बनाने के अन्य तरीके हैं। वे कैसे संबंधित हैं, यह देखने के लिए प्रत्येक चरण के पीछे का अर्थ समझें। आप इन सिद्धांतों का उपयोग करके एक सरल पेंडुलम आंदोलन का वर्णन कर सकते हैं, लेकिन आपको अन्य कारकों को भी ध्यान में रखना चाहिए जो सरल पेंडुलम सिद्धांत को प्रभावित कर सकते हैं।

पेंडुलम आंदोलन को प्रभावित करने वाले कारक

यदि आप इस व्युत्पत्ति के परिणाम की तुलना करते हैं = (t) = =_{अधिकतम}cos (t (L / g)²) एक साधारण हार्मोनिक ऑसिलेटर के समीकरण (_ t (t) = simple)_{अधिकतम}cos (2 settingt / T)) b_y उन्हें एक दूसरे के बराबर सेट करते हैं, आप अवधि T के लिए एक समीकरण प्राप्त कर सकते हैं।

ध्यान दें कि यह समीकरण टी = 2 L (एल / जी)^-1/2 बड़े पैमाने पर निर्भर नहीं करता है म पेंडुलम का, आयाम θ_{अधिकतम}, न ही समय पर टी। इसका मतलब है कि अवधि द्रव्यमान, आयाम और समय से स्वतंत्र है, लेकिन, इसके बजाय, स्ट्रिंग की लंबाई पर निर्भर करता है। यह आपको पेंडुलम आंदोलन को व्यक्त करने का एक संक्षिप्त तरीका देता है।

पेंडुलम उदाहरण की लंबाई

एक अवधि के लिए समीकरण के साथ टी = 2 L (एल / जी) __^-1/2, आप समीकरण प्राप्त करने के लिए L = (T / 2_ the) प्राप्त कर सकते हैं² / g_ और विकल्प 1 सेकंड के लिए टी तथा 9.8 मी। / से² के लिये जी प्राप्त करना ल = 0.0025 मी। ध्यान रखें कि सरल पेंडुलम सिद्धांत के ये समीकरण मान लेते हैं कि स्ट्रिंग की लंबाई घर्षण रहित और द्रव्यमान रहित है। उन कारकों को ध्यान में रखने के लिए अधिक जटिल समीकरणों की आवश्यकता होगी।

सरल पेंडुलम परिभाषा

आप पेंडुलम को पीछे के कोण से खींच सकते हैं θ इसे आगे-पीछे झूलने दें, ताकि बसंत की तरह यह दोलन कर सके। एक साधारण पेंडुलम के लिए आप एक सरल हार्मोनिक ऑसिलेटर की गति के समीकरणों का उपयोग करके इसका वर्णन कर सकते हैं। गति का समीकरण कोण के छोटे मूल्यों के लिए अच्छी तरह से काम करता है और आयामअधिकतम कोण, क्योंकि साधारण पेंडुलम मॉडल सन्निकटन पर निर्भर करता है पाप (θ) ≈ θ कुछ पेंडुलम कोण के लिए θ. जैसा कि मान कोण और आयाम लगभग 20 डिग्री से बड़े हो जाते हैं, यह सन्निकटन काम नहीं करता है।

इसे स्वयं के लिए प्रयास करें। एक पेंडुलम एक बड़े प्रारंभिक कोण के साथ झूल रहा है θ अभिप्रेरित नहीं है कि आप नियमित रूप से इसका वर्णन करने के लिए एक सरल हार्मोनिक ऑसिलेटर का उपयोग करने की अनुमति दें। एक छोटे से प्रारंभिक कोण पर θ, पेंडुलम एक नियमित रूप से, दोलनशील गति के लिए और अधिक आसानी से संपर्क करता है। क्योंकि एक पेंडुलम के द्रव्यमान का उसकी गति पर कोई असर नहीं होता है, भौतिकविदों ने यह साबित किया है कि सभी पेंडुलम में दोलन कोणों के लिए एक ही अवधि है - पेंडुलम के केंद्र के बीच का कोण अपने उच्चतम बिंदु पर और पेंडुलम के केंद्र के बीच का कोण - इसकी रुकी हुई स्थिति में - कम 20 डिग्री से।

गति में एक पेंडुलम के सभी व्यावहारिक उद्देश्यों के लिए, पेंडुलम अंततः विघटित होगा और स्ट्रिंग और इसके बन्धन बिंदु के बीच घर्षण के कारण ऊपर और साथ ही पेंडुलम और इसके चारों ओर हवा के बीच वायु प्रतिरोध के कारण रुक जाएगा।

पेंडुलम आंदोलन के व्यावहारिक उदाहरणों के लिए, अवधि और वेग का उपयोग उस सामग्री के प्रकार पर निर्भर करेगा जो घर्षण और वायु प्रतिरोध के इन उदाहरणों का कारण होगा। यदि आप इन बलों के लिए लेखांकन के बिना सैद्धांतिक पेंडुलम दोलन व्यवहार पर गणना करते हैं, तो यह असीम रूप से एक पेंडुलम दोलन के लिए जिम्मेदार होगा।

पेंडुलम में न्यूटन के नियम

न्यूटन का पहला कानून बलों के जवाब में वस्तुओं के वेग को परिभाषित करता है। कानून कहता है कि यदि कोई वस्तु एक विशिष्ट गति से और एक सीधी रेखा में चलती है, तो वह उस गति से और एक सीधी रेखा में चलती रहेगी, असीम रूप से, जब तक कोई अन्य बल उस पर कार्य नहीं करता है। एक गेंद को सीधे आगे फेंकने की कल्पना करें - गेंद पृथ्वी के ऊपर और ऊपर जाएगी अगर वायु प्रतिरोध और गुरुत्वाकर्षण ने उस पर कार्रवाई नहीं की। इस कानून से पता चलता है कि चूंकि एक पेंडुलम पक्ष की ओर बढ़ता है और ऊपर और नीचे नहीं होता है और इस पर अभिनय करने वाले बल नहीं होते हैं।

न्यूटन दूसरा कानून पेंडुलम पर शुद्ध बल का निर्धारण करने के लिए उपयोग किया जाता है, जो गुरुत्वाकर्षण बल को स्ट्रिंग के बल के बराबर स्थापित करता है जो पेंडुलम पर वापस खींचता है। एक दूसरे के बराबर इन समीकरणों को सेट करना आपको पेंडुलम के लिए गति के समीकरणों को प्राप्त करने देता है।

न्यूटन के तीसरे नियम में कहा गया है कि प्रत्येक क्रिया में समान बल की प्रतिक्रिया होती है। यह कानून यह दिखाते हुए पहले कानून के साथ काम करता है कि यद्यपि द्रव्यमान और गुरुत्वाकर्षण स्ट्रिंग तनाव वेक्टर के ऊर्ध्वाधर घटक को रद्द कर देते हैं, लेकिन क्षैतिज घटक को रद्द नहीं करता है। इस कानून से पता चलता है कि एक पेंडुलम पर काम करने वाले बल एक दूसरे को रद्द कर सकते हैं।

भौतिक विज्ञानी न्यूटन का उपयोग पहले, दूसरे और तीसरे कानून में करते हैं ताकि यह साबित हो सके कि क्षैतिज स्ट्रिंग तनाव जन या गुरुत्वाकर्षण की परवाह किए बिना पेंडुलम को स्थानांतरित करता है। एक साधारण पेंडुलम के नियम न्यूटन के विचारों को गति के तीन नियमों का पालन करते हैं।