एक प्रत्यक्ष और एक व्युत्क्रम संबंध के बीच अंतर क्या है?

विषय

• टीएल; डीआर (बहुत लंबा; डिडंट रीड)
• पृष्ठभूमि: x के साथ y कैसे भिन्न होता है?
• प्रत्यक्ष संबंध
• उलटे रिश्ते
• प्रत्यक्ष बनाम विलोम संबंध: अंतर

दो चर के बीच संबंधों को समझना अधिकांश विज्ञान के लिए लक्ष्य है। क्या आपके मन में एक विशिष्ट वैज्ञानिक प्रश्न है जैसे: वैश्विक तापमान का क्या होता है यदि वायुमंडल में कार्बन डाइऑक्साइड की मात्रा बढ़ जाती है, या जब आप स्रोत से दूर जाते हैं, तो गुरुत्वाकर्षण की शक्ति कैसे बदलती है, या आप अधिक हैं यदि आप इन रिश्तों का वर्णन करना चाहते हैं, तो एक गणितीय गणितीय सेटिंग में रुचि रखते हैं, प्रत्यक्ष और व्युत्क्रम रिश्तों के बीच अंतर का पता लगाना आवश्यक है। संक्षेप में, प्रत्यक्ष संबंध एक साथ बढ़ते या घटते हैं, लेकिन उलटे रिश्ते विपरीत दिशाओं में चलते हैं।

टीएल; डीआर (बहुत लंबा; डिडंट रीड)

प्रत्यक्ष संबंध में, एक मात्रा में वृद्धि दूसरे में इसी कमी की ओर ले जाती है। इसका गणितीय सूत्र है y = KX, कहाँ पे क एक स्थिर है। एक सर्कल के लिए, परिधि = p × × व्यास, जो एक स्थिर के रूप में pi के साथ एक सीधा संबंध है। एक बड़े व्यास का मतलब एक बड़ा परिधि है।

एक व्युत्क्रम संबंध में, एक मात्रा में वृद्धि दूसरे में एक समान कमी की ओर ले जाती है। गणितीय रूप से, इसे इस रूप में व्यक्त किया जाता है y = क/एक्स। एक यात्रा के लिए, यात्रा समय = दूरी, गति, जो एक निरंतर के रूप में यात्रा की गई दूरी के साथ एक विपरीत संबंध है। तेज़ यात्रा का मतलब है छोटी यात्रा का समय।

पृष्ठभूमि: x के साथ y कैसे भिन्न होता है?

प्रत्यक्ष और विलोम रिश्तों से निपटने वाले वैज्ञानिक और गणितज्ञ सामान्य सवाल का जवाब दे रहे हैं कि कैसे y साथ बदलता एक्स? यहाँ, एक्स तथा y मूल रूप से कुछ भी हो सकता है कि दो चर के लिए खड़े हो जाओ। उदाहरण के लिए, एक गेंद कितनी ऊँचाई तक जाती है (y) पर निर्भर करता है कि यह कितना ऊंचा गिरा है (एक्स)? रिवाज के अनुसार, एक्स स्वतंत्र चर है और y आश्रित चर है। का मूल्य है y के मूल्य पर निर्भर करता है एक्स, अन्य तरीके से नहीं, और गणितज्ञ का कुछ नियंत्रण है एक्स (उदाहरण के लिए, वह गेंद को गिराने के लिए ऊँचाई चुन सकती है)। जब कोई सीधा या उलटा संबंध होता है, एक्स तथा y किसी न किसी तरह से एक दूसरे के आनुपातिक हैं।

प्रत्यक्ष संबंध

एक सीधा संबंध इस अर्थ में आनुपातिक है कि जब एक चर बढ़ता है, तो दूसरा करता है। अंतिम अनुभाग से उदाहरण का उपयोग करना, जिसमें से आप एक गेंद को छोड़ते हैं, उच्च वह वापस ऊपर उछलता है। एक बड़े व्यास के साथ एक सर्कल में एक बड़ा परिधि होगा। यदि आप स्वतंत्र चर बढ़ाते हैं (एक्स, जैसे कि वृत्त का व्यास या बॉल ड्रॉप की ऊंचाई), आश्रित चर भी बढ़ता है और इसके विपरीत।

एक सीधा संबंध रैखिक है। एक वृत्त की परिधि है सी = π_D_, कहाँ पे सी मतलब परिधि और डी व्यास का मतलब है। पाई हमेशा समान होती है, इसलिए यदि आप के मूल्य को दोगुना करते हैं डी, का मूल्य सी युगल भी। यदि आप इस रिश्ते का ग्राफ बनाते हैं, तो यह शून्य परिधि के साथ एक सीधी रेखा के बराबर होगा डी = 0, 3.14 बजे डी = 1 और 31.4 बजे डी = 10. ग्राफ का ढाल आपको स्थिरांक का मान बताता है।

उलटे रिश्ते

उलटे रिश्ते अलग तरह से काम करते हैं। यदि आप बढ़ाते हैं एक्स, का मूल्य y घट जाती है। उदाहरण के लिए, यदि आप अपने गंतव्य पर अधिक तेज़ी से जाते हैं, तो आपकी यात्रा का समय कम हो जाएगा। इस उदाहरण में, एक्स आपकी गति है और y यात्रा का समय है। अपनी गति को दोगुना करने से यात्रा का समय आधा हो जाता है, और गति को दस गुना बढ़ाने से यात्रा का समय दस गुना कम हो जाता है।

गणितीय रूप से, इस प्रकार के संबंधों का रूप है: y = क / एक्स, कहाँ पे क कुछ स्थिर है (प्रत्यक्ष संबंध उदाहरण में पाई जैसी ही भूमिका को भरना)। उलटे रिश्ते हालांकि सीधी रेखाएं नहीं हैं। जैसे-जैसे आप बढ़ना शुरू करते हैं एक्स, y वास्तव में जल्दी से घट जाती है, लेकिन जैसे-जैसे आप बढ़ते रहते हैं एक्स की कमी की दर y धीमा हो जाता है।

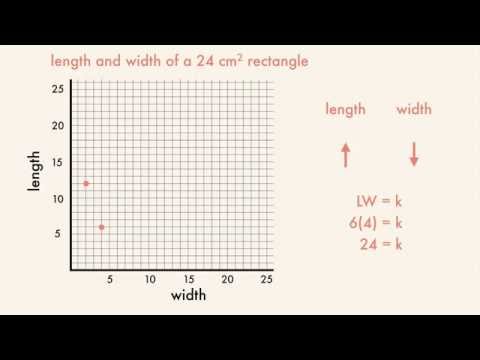
उदाहरण के लिए, यदि एक्स आयत के किनारों के एक जोड़े की लंबाई है, y पक्षों की अन्य जोड़ी की लंबाई है, और क क्षेत्र है, सूत्र क = xy वैध है, इसलिए y = क ÷ एक्स। इस मामले में, y के विपरीत है एक्स। एक क्षेत्र के लिए क = 12, यह देता है y = 12 ÷ एक्स। के लिये एक्स = 3, यह दिखाता है y = 4. के लिए एक्स = 6, तब y = 2. के लिए एक्स = 12, फिर y = 1. पहले 3 में वृद्धि हुई एक्स कम हो जाती है y 2 से, लेकिन फिर 6 की वृद्धि हुई एक्स केवल घटता है y 1. 1. यही कारण है कि उलटे रिश्ते घटते घटते हैं जो आपके साथ आगे बढ़ते हैं।

प्रत्यक्ष बनाम विलोम संबंध: अंतर

प्रत्यक्ष संबंधों में, वृद्धि हुई है एक्स एक समान आकार में वृद्धि की ओर जाता है y, और कमी का विपरीत प्रभाव पड़ता है। यह एक सीधी रेखा का ग्राफ बनाता है। उलटे रिश्तों में, बढ़ते हुए एक्स में एक इसी कमी की ओर जाता है y, और में कमी एक्स में वृद्धि की ओर जाता है y। यह एक घुमावदार ग्राफ बनाता है जहां गिरावट पहले तेजी से होती है लेकिन बड़े मूल्यों के लिए धीमी हो जाती है एक्स.