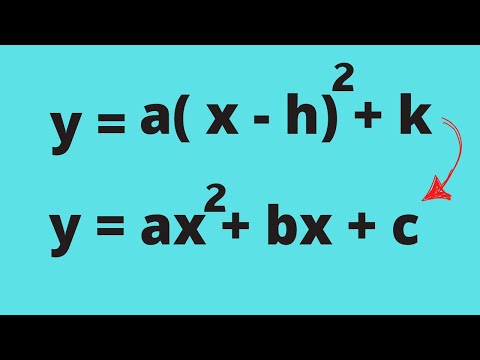
विषय
परबोला समीकरण y = ax ^ 2 + bx + c के मानक रूप में लिखे गए हैं। यह प्रपत्र आपको बता सकता है कि क्या परवलय ऊपर या नीचे खुलता है और, एक साधारण गणना के साथ, आपको बता सकता है कि समरूपता का अक्ष क्या है। जबकि यह एक सामान्य रूप में परवलय के लिए एक समीकरण देखने के लिए है, एक और रूप है जो आपको परवलय के बारे में थोड़ी अधिक जानकारी दे सकता है। वर्टेक्स फॉर्म आपको परवलय के शीर्ष को बताता है कि यह किस तरह से खुलता है, और क्या यह एक विस्तृत या संकीर्ण परवल है।
Y = ax ^ 2 + bx + c के मानक समीकरण का उपयोग करके, a और b गुणांकों को सूत्र x = -b / 2a में प्लग करके शीर्ष बिंदु का x मान ज्ञात करें।
उदाहरण के लिए:
y = 3x ^ 2 + 6x + 8 x = -6 / (2 * 3) = -6/6 = -1
मूल मान में x का पाया मान y का मान ज्ञात करें।
y = 3 (-1) ^ 2 + 6 (-1) +8 y = 3-6 + 8 y = 5
X और y के मान शीर्ष के निर्देशांक हैं। इस मामले में, शीर्ष (-1,5) पर है।
समीकरण y = a (x-h) ^ 2 + k, जहां h x- मान है और k y- मान है, में शीर्ष निर्देशांक डालें। मूल समीकरण से आता है का मान।
y = 3 (x + 1) ^ 2 + 5 यह परवलय समीकरण का शीर्ष रूप है।
(एच समीकरण में एक +1 है क्योंकि -1 के सामने एक नकारात्मक इसे सकारात्मक बनाता है।)
शीर्ष प्रपत्र को वापस मानक रूप में परिवर्तित करने के लिए, बस द्विपद को वर्गित करें, ए वितरित करें और स्थिरांक जोड़ें।
y = 3 (x + 1) ^ 2 + 5 y = 3 (x ^ 2 + 2x + 1) +5 y = 3x ^ 2 + 6x + 3 + 5 y = 3x ^ 2 + 6x + 8
यह समीकरण का मूल मानक रूप है।