चतुर्भुज की परिधि की गणना कैसे करें

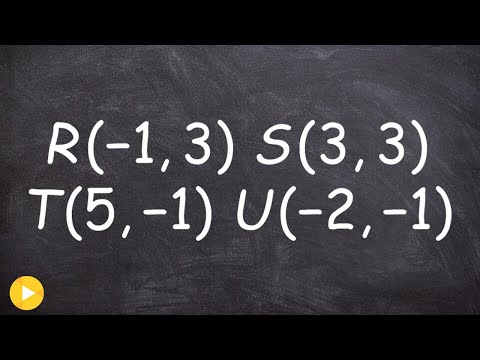
विषय

• एक वर्ग और एक गर्भ के परिधि
• एक आयत और समांतर चतुर्भुज की परिधि
• एक ट्रेपेज़ॉइड की परिधि
• एक अनियमित चतुर्भुज की परिधि
• साइड लंबाई निर्धारित करने के लिए निर्देशांक का उपयोग करना

एक चतुर्भुज की परिधि की गणना करने के लिए, चार पक्षों का माप जोड़ें। परिधि एक आकृति के चारों ओर की दूरी है। वास्तविक जीवन के अनुप्रयोगों में, परिधि एक यार्ड के चारों ओर की बाड़ या चित्र के चारों ओर फ्रेम है। परिधि दो-आयामी आकृति के चारों ओर फैली हुई है। एक चतुर्भुज एक बहुभुज है जिसके चार पक्ष और चार कोण हैं। सबसे सामान्य प्रकार के चतुर्भुज में एक वर्ग, एक आयत, एक रोम्बस, एक ट्रेपोज़ॉइड और एक समांतर चतुर्भुज शामिल हैं।

एक वर्ग और एक गर्भ के परिधि

एक वर्ग और एक रोम्बस में प्रत्येक के चार बराबर भाग होते हैं, लेकिन एक वर्ग में चार समकोण होते हैं। परिधि के लिए सूत्र दोनों आकृतियों के लिए समान है, और आपको केवल एक पक्ष के माप को जानने की आवश्यकता है। सूत्र है 4 x s = परिधि, कहाँ पे रों एक तरफ की लंबाई का प्रतिनिधित्व करता है। यदि एक तरफ का माप 2 इंच है, 2 को 4 से गुणा करें। परिधि 8 इंच है।

एक आयत और समांतर चतुर्भुज की परिधि

एक आयत और समांतर चतुर्भुज की परिधि के सूत्र समान हैं, क्योंकि प्रत्येक बहुभुज में समान पक्षों के दो सेट होते हैं। सूत्र है 2 (l + w) = परिधि, कहाँ पे एल लंबाई का प्रतिनिधित्व करता है और w चौड़ाई का प्रतिनिधित्व करता है। एक आयत पर विचार करें जिसकी लंबाई 2 इंच और चौड़ाई 4 इंच है। लंबाई और चौड़ाई का योग 6 है। 6 को 2 से गुणा करें और आपको 12 इंच की परिधि मिलती है।

एक ट्रेपेज़ॉइड की परिधि

एक ट्रेपोज़ॉइड का सूत्र थोड़ा अलग है, क्योंकि एक ट्रैपोज़ॉइड एक चतुर्भुज है जिसमें असमान लंबाई के दो समानांतर पक्ष हैं। दो पक्षों में एक दूसरे के बराबर लंबाई होती है। अन्य दो पक्षों की लंबाई एक-दूसरे के बराबर है, लेकिन इन दोनों पक्षों की लंबाई अन्य दो पक्षों की लंबाई से अलग है। कक्षाओं में कुछ स्कूल डेस्क ट्रेपोज़िड्स हैं।

सूत्र है a + b + c + d = परिधि। प्रत्येक अक्षर एक अलग पक्ष या आकृति के आधार से मेल खाता है। उदाहरण के लिए, मान लीजिए कि एक ट्रेपोज़ॉइड में किनारे की माप 2, 3, 2 और 5 इंच है। परिधि 2 + 3 + 2 + 5 है, जो 12 इंच के बराबर है।

एक अनियमित चतुर्भुज की परिधि

एक अनियमित चतुर्भुज के लिए सूत्र - जो एक बहुभुज है जिसमें चार भुजाएं हैं जो असमान लंबाई के हैं - वही है जो एक समलम्बाकार है। सूत्र है a + b + c + d = परिधि। उदाहरण के लिए, मान लीजिए कि एक चतुर्भुज की भुजाएँ 1, 5, 3 और 4 इंच की लंबाई के साथ हैं। परिधि 1 + 5 + 3 + 4 या 13 इंच के बराबर होती है।

साइड लंबाई निर्धारित करने के लिए निर्देशांक का उपयोग करना

यदि आप केवल आकृति के निर्देशांक को जानते हैं, तो बिंदुओं के बीच की दूरी का पता लगाकर पक्ष मापें। उदाहरण के लिए, एक पक्ष के लिए अंक A और B के बीच की दूरी और दूसरे पक्ष के लिए B और C के बीच की दूरी का पता लगाएं। फिर, परिधि निर्धारित करने के लिए उचित माप में पक्ष माप प्लग करें।