विषय
- टीएल; डीआर (बहुत लंबा; डिडंट रीड)
- एक साधारण हार्मोनिक थरथरानवाला की प्राकृतिक आवृत्ति परिभाषित
- प्राकृतिक आवृत्ति की गणना
सभी दोलन गति - एक गिटार स्ट्रिंग, एक छड़ी के हिलने, या एक वसंत पर एक वजन के उछाल के कारण हिलने की गति - एक प्राकृतिक आवृत्ति है। गणना के लिए मूल स्थिति में वसंत पर एक द्रव्यमान शामिल होता है, जो एक सरल हार्मोनिक ऑसिलेटर है। अधिक जटिल मामलों के लिए, आप भिगोना (दोलन धीमा करना) के प्रभावों को जोड़ सकते हैं या ड्राइविंग बलों या खाते में लिए गए अन्य कारकों के साथ विस्तृत मॉडल बना सकते हैं। हालांकि, एक सरल प्रणाली के लिए प्राकृतिक आवृत्ति की गणना करना आसान है।
टीएल; डीआर (बहुत लंबा; डिडंट रीड)
सूत्र का उपयोग करके एक सरल हार्मोनिक थरथरानवाला की प्राकृतिक आवृत्ति की गणना करें:
च = √(क / म) ÷ 2π
जिस सिस्टम के लिए आप स्पॉट में विचार कर रहे हैं, उसके लिए स्प्रिंग कंटीन्यू डालें क, और के लिए दोलन द्रव्यमान म, और फिर मूल्यांकन करें।
एक साधारण हार्मोनिक थरथरानवाला की प्राकृतिक आवृत्ति परिभाषित
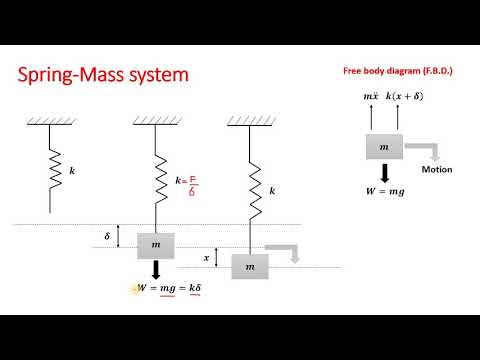
द्रव्यमान के साथ अंत में जुड़ी हुई गेंद के साथ एक वसंत की कल्पना करें म। जब सेटअप स्थिर होता है, तो वसंत आंशिक रूप से फैला होता है, और पूरा सेटअप संतुलन की स्थिति में होता है, जहां विस्तारित वसंत से तनाव गुरुत्वाकर्षण के बल को गेंद को नीचे की ओर खींचता है। गेंद को इस संतुलन की स्थिति से दूर ले जाना या तो वसंत में तनाव जोड़ता है (यदि आप इसे नीचे की तरफ खींचते हैं) या गुरुत्वाकर्षण को वसंत से गेंद को तनाव के बिना खींचने का अवसर देता है इसे (यदि आप गेंद को ऊपर की ओर धकेलते हैं)। दोनों ही मामलों में, गेंद संतुलन स्थिति के चारों ओर दोलन करना शुरू कर देती है।
प्राकृतिक आवृत्ति इस दोलन की आवृत्ति है, जिसे हर्ट्ज़ (हर्ट्ज) में मापा जाता है। यह आपको बताता है कि प्रति सेकंड कितने दोलन होते हैं, जो वसंत के गुणों और उससे जुड़ी गेंद के द्रव्यमान पर निर्भर करता है। फंसे हुए गिटार के तार, एक वस्तु द्वारा छड़ें और कई अन्य सिस्टम एक प्राकृतिक आवृत्ति पर दोलन करते हैं।
प्राकृतिक आवृत्ति की गणना
निम्नलिखित अभिव्यक्ति एक सरल हार्मोनिक थरथरानवाला की प्राकृतिक आवृत्ति को परिभाषित करती है:
च = ω /2π
कहाँ पे ω दोलन की कोणीय आवृत्ति है, जिसे रेडियन / सेकंड में मापा जाता है। निम्नलिखित अभिव्यक्ति कोणीय आवृत्ति को परिभाषित करती है:
ω = √(क / म)
तो इसका मतलब है:
च = √(क / म) ÷ 2π
यहाँ, क सवाल में वसंत के लिए वसंत स्थिरांक है और म गेंद का द्रव्यमान है। वसंत स्थिरांक को न्यूटन / मीटर में मापा जाता है। उच्च स्थिरांक वाले स्प्रिफ़ स्टिफ़र हैं और विस्तार के लिए अधिक बल लेते हैं।
उपरोक्त समीकरण का उपयोग करके प्राकृतिक आवृत्ति की गणना करने के लिए, पहले अपने विशिष्ट सिस्टम के लिए वसंत स्थिरांक का पता लगाएं। आप प्रयोग के माध्यम से वास्तविक प्रणालियों के लिए वसंत स्थिर पा सकते हैं, लेकिन अधिकांश समस्याओं के लिए, आपको इसके लिए एक मूल्य दिया जाता है। इस मान को उस स्थान के लिए डालें क (इस उदाहरण में, क = 100 N / m), और इसे वस्तु के द्रव्यमान से विभाजित करें (उदाहरण के लिए, म = 1 किलो)। फिर, इसे 2π से विभाजित करने से पहले, परिणाम का वर्गमूल लें। चरणों के माध्यम से जा रहे हैं:
च = = (100 एन / एम / 1 किग्रा) π 2 N
= = (100 एस)−2) ÷ 2π
= 10 हर्ट्ज π 2π
= 1.6 हर्ट्ज
इस मामले में, प्राकृतिक आवृत्ति 1.6 हर्ट्ज है, जिसका अर्थ है कि सिस्टम प्रति सेकंड डेढ़ गुना अधिक समय में दोलन करेगा।