विषय
रोजमर्रा के प्रवचन में, "गति" और "वेग" का उपयोग अक्सर एक-दूसरे से किया जाता है। भौतिकी में, हालांकि, इन शब्दों के विशिष्ट और विशिष्ट अर्थ हैं। "गति" अंतरिक्ष में किसी वस्तु के विस्थापन की दर है, और यह केवल विशिष्ट इकाइयों (अक्सर मीटर प्रति सेकंड या मील प्रति घंटे) के साथ एक संख्या द्वारा दी जाती है। दूसरी ओर वेग, एक दिशा के लिए युग्मित गति है। गति, फिर, एक अदिश राशि कहलाती है, जबकि वेग एक सदिश राशि है।
जब कोई कार राजमार्ग या बेसबॉल के साथ घूम रही होती है, तो हवा में घूमती है, तो जमीन के संदर्भ में इन वस्तुओं की गति को मापा जाता है, जबकि वेग में अधिक जानकारी शामिल होती है। उदाहरण के लिए, यदि आप संयुक्त राज्य अमेरिका के पूर्वी तट पर अंतरराज्यीय 95 पर 70 मील प्रति घंटे की गति से यात्रा कर रहे हैं, तो यह जानना भी उपयोगी है कि क्या यह उत्तर-पूर्व की ओर बोस्टन या दक्षिण की ओर फ्लोरिडा की ओर है। बेसबॉल के साथ, आप जानना चाह सकते हैं कि क्या इसका y- निर्देशांक अपने x- समन्वय (एक फ्लाई बॉल) की तुलना में अधिक तेजी से बदल रहा है या यदि रिवर्स सही है (एक लाइन ड्राइव)। लेकिन टायर के घूमने या बेसबॉल के घूमने (स्पिन) के बारे में क्या कार और गेंद अपने अंतिम गंतव्य की ओर बढ़ते हैं? इस प्रकार के प्रश्नों के लिए, भौतिकी की अवधारणा प्रदान करता है कोणीय गति.
मूल बातें
चीजें तीन-आयामी भौतिक स्थान से दो मुख्य तरीकों से गुजरती हैं: अनुवाद और रोटेशन। अनुवाद संपूर्ण वस्तु का एक स्थान से दूसरे स्थान पर विस्थापन है, जैसे न्यूयॉर्क शहर से लॉस एंजिल्स के लिए कार चलाना। दूसरी ओर, रोटेशन, एक निश्चित बिंदु के आसपास किसी वस्तु का चक्रीय गति है। कई वस्तुओं, जैसे कि उपरोक्त उदाहरण में बेसबॉल, एक ही समय में दोनों प्रकार के आंदोलन को प्रदर्शित करते हैं; एक मक्खी की गेंद के रूप में आउटफील्ड बाड़ की ओर घर की थाली से हवा के माध्यम से ले जाया गया, यह भी अपने स्वयं के केंद्र के आसपास दी गई दर पर घूमता है।
इन दो प्रकार की गति का वर्णन अलग भौतिकी समस्याओं के रूप में किया जाता है; वह यह है कि जब गेंद अपने प्रारंभिक प्रक्षेपण कोण और जिस गति से बल्ले को छोड़ती है, उसके आधार पर गेंद हवा के माध्यम से यात्रा करती है, तो आप इसके रोटेशन को नजरअंदाज कर सकते हैं, और इसके रोटेशन की गणना करते समय आप इसे एक में बैठे समझ सकते हैं। वर्तमान उद्देश्यों के लिए जगह।
कोणीय वेग समीकरण
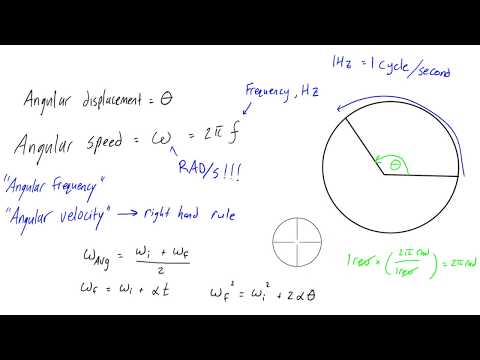
सबसे पहले, जब आप "कोणीय" किसी भी चीज़ के बारे में बात कर रहे हों, तो यह वेग या कुछ अन्य भौतिक मात्रा हो, तो उसे पहचानें, क्योंकि आप कोणों के साथ काम कर रहे हैं, तो आप मंडलियों या उसके भागों में यात्रा करने की बात कर रहे हैं। आप ज्यामिति या त्रिकोणमिति से याद कर सकते हैं कि एक वृत्त की परिधि इसके व्यास के स्थिर पी, या है πd। (Pi का मान लगभग 3.14159 है।) यह सामान्यतः वृत्तों की त्रिज्या के संदर्भ में व्यक्त किया जाता है आर, जो आधा व्यास है, परिधि बना रहा है 2πr.
इसके अलावा, आपने शायद कहीं भी सीखा है कि एक सर्कल में 360 डिग्री (360 °) होता है। यदि आप एक वृत्त के साथ दूरी एस को स्थानांतरित करते हैं, तो कोणीय विस्थापन a एस / आर के बराबर है। एक पूर्ण क्रांति, तब 2πr / r देता है, जो सिर्फ 2π छोड़ देता है। इसका मतलब है कि कोण कम है कि 360 ° पाई के संदर्भ में, या दूसरे शब्दों में, रेडियन के रूप में व्यक्त किया जा सकता है।
जानकारी के इन सभी टुकड़ों को एक साथ लेते हुए, आप डिग्री के अलावा इकाइयों में कोणों, या एक सर्कल के कुछ हिस्सों को व्यक्त कर सकते हैं:
360 ° = (2 °) रेडियन, या
1 रेडियन = (360 ° / 2π) = 57.3 °,
जबकि रैखिक वेग को प्रति इकाई समय लंबाई में व्यक्त किया जाता है, कोणीय वेग को प्रति इकाई समय, आमतौर पर प्रति सेकंड रेडियन में मापा जाता है।
यदि आप जानते हैं कि एक कण एक वृत्ताकार पथ में वेग के साथ घूम रहा है v कुछ दूरी पर आर सर्कल के केंद्र से, की दिशा के साथ v हमेशा वृत्त की त्रिज्या के लंबवत होने के बाद, कोणीय वेग लिखा जा सकता है
r = वी / आर,
कहाँ पे ω ग्रीक अक्षर ओमेगा है। कोणीय वेग इकाइयाँ प्रति सेकंड रेडियन हैं; आप इस इकाई को "पारस्परिक सेकंड" के रूप में भी मान सकते हैं, क्योंकि v / r पैदावार m / s m, या s द्वारा विभाजित है-1, जिसका अर्थ है कि रेडियन तकनीकी रूप से एक इकाई रहित मात्रा हैं।
घूर्णी गति समीकरण
कोणीय त्वरण सूत्र को कोणीय वेग सूत्र के रूप में एक ही आवश्यक तरीके से प्राप्त किया जाता है: यह केवल वृत्त की त्रिज्या के लिए लंबवत दिशा में रैखिक त्वरण है (समान रूप से, किसी भी बिंदु पर परिपत्र पथ पर एक स्पर्शरेखा के साथ इसका त्वरण) विभाजित है वृत्त या वृत्त के भाग की त्रिज्या द्वारा, जो है:
α = एटी/ r
इसके द्वारा भी दिया गया है:
α = ω / t
क्योंकि परिपत्र गति के लिए, एटी = =r / t = v / t।
α, जैसा कि आप शायद जानते हैं, ग्रीक अक्षर "अल्फ़ा" है। सबस्क्रिप्ट "t" यहाँ "स्पर्शरेखा" को दर्शाता है।
उत्सुकता से पर्याप्त है, हालांकि, घूर्णी गति एक अन्य प्रकार के त्वरण का दावा करती है, जिसे सेंट्रिपेटल ("केंद्र-मांग") त्वरण कहा जाता है। यह अभिव्यक्ति द्वारा दिया गया है:
एसी = वी2/ r
यह त्वरण उस बिंदु की ओर निर्देशित होता है जिसके चारों ओर प्रश्न में वस्तु घूमती है। यह अजीब लग सकता है, क्योंकि ऑब्जेक्ट त्रिज्या के बाद से इस केंद्रीय बिंदु के करीब नहीं हो रहा है आर निश्चित है। सेंट्रिपेटल एक्सेलेरेशन को फ्री-फॉल के रूप में सोचें, जिसमें जमीन से टकराने वाली वस्तु का कोई खतरा नहीं है, क्योंकि ऑब्जेक्ट को इस ओर खींचते हुए (आमतौर पर गुरुत्वाकर्षण) पहले समीकरण द्वारा वर्णित स्पर्शरेखा (रैखिक) त्वरण द्वारा बिल्कुल ऑफसेट होता है। यह अनुभाग। अगर एसी के बराबर नहीं थे एटीऑब्जेक्ट या तो अंतरिक्ष में उड़ जाएगा या जल्द ही सर्कल के बीच में दुर्घटनाग्रस्त हो जाएगा।
संबंधित मात्राएँ और अभिव्यक्तियाँ
हालांकि कोणीय वेग आमतौर पर व्यक्त किया जाता है, जैसा कि कहा गया है, प्रति सेकंड रेडियन में, ऐसे उदाहरण हो सकते हैं जिसमें किसी समस्या को हल करने से पहले डिग्री से प्रति सेकंड का उपयोग करना या इसके विपरीत डिग्री से रेडियन में परिवर्तित करना बेहतर होता है।
आपको बता दें कि एक प्रकाश स्रोत एक स्थिर वेग पर हर सेकंड 90 ° घूमता है। रेडियंस में इसका कोणीय वेग क्या है?
सबसे पहले, याद रखें कि 2, रेडियन = 360 °, और एक अनुपात सेट करें:
360/2 90 = 90 / x
360x = 180x
x = π = π / 2
इसका उत्तर प्रति सेकंड एक आधा पीआई रेडियन है।
यदि आपको आगे बताया गया है कि प्रकाश किरण की सीमा 10 मीटर है, तो बीम के रैखिक वेग की नोक क्या होगी v, इसके कोणीय त्वरण α और इसका केंद्रबिंदु त्वरण एसी?
के लिए हल करने के लिए vऊपर से, v = ,r, जहां π = 2/2 और r = 10m:
((/ 2) (10) = 5π रेड / एस = 15.7 एम / एस
के लिए हल करने के लिए α, बस हर समय एक और इकाई जोड़ें।
α = 5π रेड / एस2
(ध्यान दें कि यह केवल उन समस्याओं के लिए काम करता है जिसमें कोणीय वेग स्थिर है।)
अंत में, ऊपर से भी, एसी = वी2/ आर = (१५..7)2/ 10 = 24.65 मीटर / सेकंड2.
कोणीय वेग बनाम रैखिक वेग
पिछली समस्या पर बिल्डिंग, अपने आप को एक बहुत बड़े मीरा-गो-राउंड पर कल्पना करें, 10 किलोमीटर (10,000 मीटर) की संभावना वाले त्रिज्या के साथ। यह मेरी-गो-राउंड हर 1 मिनट और 40 सेकंड, या हर 100 सेकंड में एक पूर्ण क्रांति करता है।
कोणीय वेग के बीच अंतर का एक परिणाम, जो रोटेशन के अक्ष से दूरी से स्वतंत्र है, और रैखिक परिपत्र वेग, जो नहीं है, दो लोगों को एक ही अनुभव कर रहा है ω काफी हद तक अलग-अलग शारीरिक अनुभव हो सकते हैं। यदि आप केंद्र से 1 मीटर की दूरी पर होते हैं यदि यह स्थानिक, बड़े पैमाने पर मीरा-गो-राउंड, आपका रैखिक (स्पर्शरेखा) वेग है:
ωr = (2π rad / 100 s) (1 m) = 0.0628 m / s, या 6.29 cm (3 इंच से कम) प्रति सेकंड।
लेकिन अगर आप इस राक्षस के रिम पर हैं, तो आपका रैखिक वेग है:
(r = (2π रेड / 100 एस) (10,000 मीटर) = 628 मीटर / सेकंड। लगभग 1,406 मील प्रति घंटा, एक गोली से भी तेज। डटे रहो!