कैसे पाएं Centripetal Force

विषय

• टीएल; डीआर (बहुत लंबा; डिडंट रीड)
• क्या है Centripetal Force?
• Centripetal Force और Centripetal Acceleration के लिए फॉर्मूला
• टिप्स
• अधूरी जानकारी के साथ Centripetal Force ढूँढना

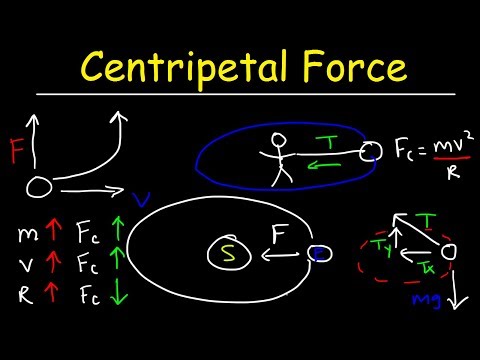
किसी वृत्त में गति करने वाली कोई भी वस्तु गतिमान है, भले ही उसकी गति समान रहे। यह उल्टा लग सकता है क्योंकि आप गति में बदलाव के बिना त्वरण कैसे कर सकते हैं? वास्तव में, क्योंकि त्वरण वेग के परिवर्तन की दर है, और वेग में गति और गति की दिशा शामिल है, त्वरण के बिना परिपत्र गति होना असंभव है। न्यूटन के दूसरे नियम से, कोई भी त्वरण (ए) एक बल से जुड़ा हुआ है (एफ) द्वारा एफ = मा, और परिपत्र गति के मामले में, प्रश्न में बल को सेंट्रिपेटल बल कहा जाता है। इसे पूरा करना एक सरल प्रक्रिया है, लेकिन आपको अपनी जानकारी के आधार पर विभिन्न तरीकों से स्थिति के बारे में सोचना पड़ सकता है।

टीएल; डीआर (बहुत लंबा; डिडंट रीड)

सूत्र का उपयोग करके केन्द्रक बल ज्ञात करें:

एफ = mv² / आर

यहाँ, एफ बल का संदर्भ देता है, म वस्तु का द्रव्यमान है, v वस्तु की स्पर्शरेखा की गति है, और आर उस वृत्त की त्रिज्या है जिसमें वह यात्रा करता है। यदि आप सेंट्रिपेटल फोर्स (गुरुत्वाकर्षण, उदाहरण के लिए) के स्रोत को जानते हैं, तो आप उस फोर्स के समीकरण का उपयोग करके सेंट्रिपेटल बल पा सकते हैं।

क्या है Centripetal Force?

सेंट्रिपेटल बल गुरुत्वाकर्षण बल या घर्षण बल के समान बल नहीं है। सेंट्रिपेटल बल मौजूद है क्योंकि सेंट्रिपेटल त्वरण मौजूद है, लेकिन इस बल का भौतिक कारण विशिष्ट स्थिति के आधार पर भिन्न हो सकता है।

सूर्य के चारों ओर पृथ्वी की गति पर विचार करें। भले ही इसकी कक्षा की गति स्थिर है, यह लगातार दिशा बदलता है और इसलिए त्वरण सूर्य की ओर निर्देशित होता है। न्यूटन के गति के पहले और दूसरे नियम के अनुसार यह त्वरण एक बल के कारण होना चाहिए। पृथ्वी की कक्षा के मामले में, त्वरण पैदा करने वाला बल गुरुत्वाकर्षण है।

हालांकि, यदि आप एक स्थिर गति से एक सर्कल में एक स्ट्रिंग पर एक गेंद को स्विंग करते हैं, तो बल का कारण त्वरण अलग है। इस मामले में, बल स्ट्रिंग में तनाव से है। एक अन्य उदाहरण एक कार है जो एक निरंतर गति बनाए रखती है लेकिन एक सर्कल में बदल जाती है। इस मामले में, कार के पहियों और सड़क के बीच घर्षण बल का स्रोत है।

दूसरे शब्दों में, सेंट्रिपेटल फोर्स मौजूद हैं, लेकिन उनका भौतिक कारण स्थिति पर निर्भर करता है।

Centripetal Force और Centripetal Acceleration के लिए फॉर्मूला

Centripetal त्वरण सीधे गति में वृत्त के केंद्र की ओर त्वरण का नाम है। इसके द्वारा परिभाषित किया गया है:

ए = v² / आर

कहाँ पे v वृत्त की वस्तु की गति वृत्त की स्पर्शरेखा है, और आर जिस वृत्त में यह घूम रहा है, उसकी त्रिज्या है। इस बारे में सोचें कि यदि आप एक सर्कल में एक स्ट्रिंग से जुड़ी गेंद को स्विंग कर रहे थे तो क्या होगा, लेकिन स्ट्रिंग टूट गई। गेंद जिस समय स्ट्रिंग टूटती है, सर्कल पर अपनी स्थिति से एक सीधी रेखा में उड़ जाती है और इससे आपको अंदाजा हो जाता है कि क्या है v उपरोक्त समीकरण में इसका मतलब है।

क्योंकि न्यूटन के दूसरे नियम में कहा गया है कि बल = द्रव्यमान × त्वरण, और हमारे पास ऊपर त्वरण के लिए एक समीकरण है, सेंट्रिपेटल बल हो सकता है:

एफ = mv² / आर

इस समीकरण में, म मास को संदर्भित करता है।

तो, केन्द्रक बल को खोजने के लिए, आपको वस्तु के द्रव्यमान, उस वृत्त की त्रिज्या जिसमें वह यात्रा कर रहा है, और उसकी स्पर्शरेखा की गति जानना आवश्यक है। इन कारकों के आधार पर बल खोजने के लिए उपरोक्त समीकरण का उपयोग करें। गति को स्क्वायर करें, इसे द्रव्यमान से गुणा करें और फिर परिणाम को सर्कल के त्रिज्या से विभाजित करें।

टिप्स

अधूरी जानकारी के साथ Centripetal Force ढूँढना

यदि आपके पास उपरोक्त समीकरण के लिए आवश्यक सभी जानकारी नहीं है, तो ऐसा प्रतीत हो सकता है कि शत-प्रतिशत बल खोजना असंभव है। हालांकि, यदि आप स्थिति के बारे में सोचते हैं, तो आप अक्सर यह समझ सकते हैं कि बल क्या हो सकता है।

उदाहरण के लिए, यदि आप किसी ग्रह पर किसी तारे या चंद्रमा की परिक्रमा करने वाले ग्रह पर केन्द्रित बल को खोजने की कोशिश कर रहे हैं, तो आप जानते हैं कि गुरुत्वीय बल गुरुत्वाकर्षण से आता है। इसका मतलब है कि आप गुरुत्वाकर्षण बल के लिए सामान्य समीकरण का उपयोग करके स्पर्शरेखा के वेग के बिना केन्द्रक बल पा सकते हैं:

एफ = ग्राम₁म₂ / आर²

कहाँ पे म₁ तथा म₂ जनता हैं, जी गुरुत्वाकर्षण स्थिरांक है, और आर दो जनता के बीच अलगाव है।

त्रिज्या के बिना सेंट्रिपेटल बल की गणना करने के लिए, आपको या तो अधिक जानकारी (त्रिज्या से संबंधित सर्कल की परिधि) की आवश्यकता होती है सी = 2 =_r, उदाहरण के लिए) या केन्द्रक त्वरण के लिए मान। यदि आप सेंट्रिपेटल त्वरण को जानते हैं, तो आप न्यूटन के दूसरे नियम, _F का उपयोग करके सीधे सेंट्रिपेटल बल की गणना कर सकते हैं = मा.