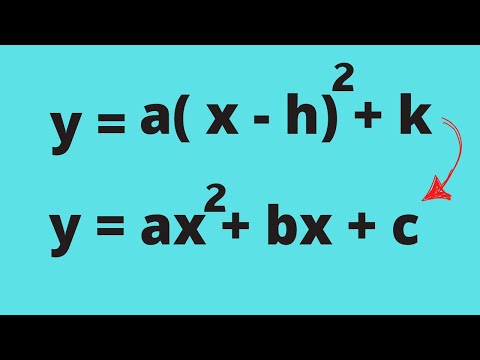
विषय
द्विघात समीकरण का मानक रूप y = ax ^ 2 + bx + c है, जहाँ a, b, और c गुणांक हैं और y और x चर हैं। जब यह मानक रूप में होता है तो द्विघात समीकरण को हल करना आसान होता है क्योंकि आप समाधान की गणना a, b और c से करते हैं। हालाँकि, यदि आपको किसी द्विघात फ़ंक्शन, या पेराबोला को रेखांकन करने की आवश्यकता है, तो समीकरण सुव्यवस्थित रूप में होने पर प्रक्रिया को सुव्यवस्थित किया जाता है। द्विघात समीकरण का शीर्ष रूप y = m (x-h) ^ 2 + k है, जो रेखा के ढलान का प्रतिनिधित्व करता है और h और k रेखा के किसी बिंदु के रूप में होता है।
कारक गुणांक
गुणांक को मानक प्रपत्र समीकरण के पहले दो शब्दों से गुणांक और इसे कोष्ठकों के बाहर रखें। फैक्टरिंग मानक रूप द्विघात समीकरणों में संख्याओं की एक जोड़ी को खोजना शामिल है जो कि बी तक जुड़ता है और एसी को गुणा करता है। उदाहरण के लिए, यदि आप 2x ^ 2 - 28x + 10 को वर्टेक्स रूप में परिवर्तित कर रहे हैं, तो आपको पहले 2 (x ^ 2 - 14x) + 10 लिखना होगा।
गुणांक को विभाजित करें
इसके बाद, कोष्ठकों के अंदर x शब्द के गुणांक को दो से विभाजित करें। वर्गमूल गुण का उपयोग करें फिर उस संख्या को वर्ग करें। उस वर्गमूल गुण विधि का उपयोग करके दोनों पक्षों के वर्गमूलों को ले कर द्विघात समीकरण हल खोजने में मदद मिलती है। उदाहरण में, कोष्ठक के अंदर x का गुणांक -14 है।
संतुलन समीकरण
कोष्ठकों के अंदर संख्या जोड़ें, और फिर समीकरण को संतुलित करने के लिए, इसे कोष्ठकों के बाहर के कारक से गुणा करें और पूरे द्विघात समीकरण से इस संख्या को घटाएं। उदाहरण के लिए, 2 (x ^ 2 - 14x) + 10 बन जाता है 2 (x ^ 2 - 14x + 49) + 10 - 98, चूंकि 49 * 2 = 98. अंत में शब्दों को जोड़कर समीकरण को सरल बनाएं। उदाहरण के लिए, 2 (x ^ 2 - 14x + 49) - 88, 10 से - 98 = -88।
शर्तें परिवर्तित करें
अंत में, कोष्ठक के अंदर की शर्तों को फॉर्म की एक चुकता इकाई में परिवर्तित करें (x - h) ^ 2। H का मान x शब्द के आधे गुणांक के बराबर है। उदाहरण के लिए, 2 (x ^ 2 - 14x + 49) - 88 2 (x - 7) ^ 2 - 88 हो जाता है। द्विघात समीकरण अब शीर्ष रूप में है। वर्बोला को वर्टेक्स रूप में रेखांकन करने के लिए फ़ंक्शन के सममित गुणों का उपयोग पहले बाईं ओर के मूल्य को चुनने और y चर को खोजने की आवश्यकता होती है। आप परबोला को ग्राफ करने के लिए डेटा पॉइंट्स को प्लॉट कर सकते हैं।