प्रकाश की गति की गणना कैसे करें

विषय

• प्रकाश प्रयोग
• खगोलीय प्रेक्षणों से प्रकाश की गति को मापना
• पानी में हवा की गति से प्रकाश की गति की तुलना करना
• प्रकाश की गति के लिए समीकरण का उपयोग करना
• लेजर का उपयोग करके एक आधुनिक माप पद्धति
• प्रकाश की गति को मापने से कोई लंबी अवधि नहीं बनती है
• प्रायोगिक उपकरण को शांत करने के लिए प्रकाश की गति का उपयोग करना
• एक वैक्यूम में प्रकाश की गति एक सार्वभौमिक निरंतर है

अपनी अंगुलियों की तस्वीर लो! उस समय में ऐसा करने के लिए, एक प्रकाश किरण लगभग सभी तरह से चंद्रमा की यात्रा करने में सक्षम थी। यदि आप अपनी उंगलियों को एक बार फिर से हिलाते हैं, तो आप यात्रा को पूरा करने के लिए बीम का समय देंगे। मुद्दा यह है कि प्रकाश वास्तव में बहुत तेजी से यात्रा करता है।

प्रकाश जल्दी से यात्रा करता है, लेकिन इसकी गति अनंत नहीं है, जैसा कि लोग 17 वीं शताब्दी से पहले मानते थे। हालांकि, लैंप, विस्फोट या अन्य साधनों का उपयोग करने के लिए गति बहुत तेज़ है जो मानव दृश्य तीक्ष्णता और मानव प्रतिक्रिया समय पर निर्भर करती है। गैलीलियो से पूछें।

प्रकाश प्रयोग

गैलीलियो ने 1638 में एक प्रयोग तैयार किया जिसमें लालटेन का इस्तेमाल किया गया था, और सबसे अच्छा निष्कर्ष जो वह प्रबंधित कर सकता था, वह यह था कि प्रकाश "असाधारण रूप से तेज" है (दूसरे शब्दों में, वास्तव में, वास्तव में तेजी से)। वह एक नंबर के साथ आने में सक्षम नहीं था, अगर वह वास्तव में, यहां तक ​​कि प्रयोग की कोशिश भी करता था। हालांकि, उन्होंने यह कहने के लिए उद्यम किया कि उनका मानना ​​है कि प्रकाश ध्वनि की तुलना में कम से कम 10 गुना तेज यात्रा करता है। वास्तव में, यह एक लाख गुना तेजी से अधिक पसंद है।

प्रकाश की गति का पहला सफल माप, जिसे भौतिक विज्ञानी सार्वभौमिक रूप से एक लोअरकेस सी द्वारा दर्शाते हैं, 1676 में ओले रोमर द्वारा बनाया गया था। उसने ज्यूपिटर चंद्रमाओं की टिप्पणियों पर अपने माप को आधारित किया। तब से, भौतिकविदों ने माप को परिष्कृत करने के लिए तारों, दांतेदार पहियों, घूर्णन दर्पण, रेडियो इंटरफेरोमीटर, गुहा प्रतिध्वनि और लेजर का अवलोकन किया है। वे अब जानते हैं सी इतनी सही तरह से कि मीटर और माप पर सामान्य परिषद मीटर आधारित है, जो एसआई प्रणाली में लंबाई की मूलभूत इकाई है, उस पर।

प्रकाश की गति एक सार्वभौमिक स्थिरांक है, इसलिए प्रकाश सूत्र की कोई गति नहीं है, दर असल। वास्तव में, यदि सी किसी भी भिन्न थे, हमारे सभी मापों को बदलना होगा, क्योंकि मीटर इस पर आधारित है। प्रकाश में तरंग विशेषताएं होती हैं, हालांकि, जिसमें आवृत्ति शामिल होती है ν और तरंग दैर्ध्य λ, और आप उन्हें इस समीकरण के साथ प्रकाश की गति से संबंधित कर सकते हैं, जिसे आप प्रकाश की गति के लिए समीकरण कह सकते हैं:

c = νλ

खगोलीय प्रेक्षणों से प्रकाश की गति को मापना

रोएमर प्रकाश की गति के लिए एक नंबर के साथ आने वाला पहला व्यक्ति था। उन्होंने ज्यूपिटर चंद्रमाओं के ग्रहणों को देखते हुए ऐसा किया, विशेष रूप से Io। वह आइओ को विशाल ग्रह के पीछे गायब होता देखेगा और फिर कितने समय के लिए फिर से प्रकट होगा। उसने तर्क दिया कि यह समय 1,000 सेकंड से अधिक तक भिन्न हो सकता है, यह इस बात पर निर्भर करता है कि बृहस्पति पृथ्वी के कितना करीब था। वह 214,000 किमी / सेकंड की प्रकाश की गति के लिए एक मूल्य के साथ आया था, जो लगभग 300,000 किमी / सेकंड के आधुनिक मूल्य के समान बॉलपार्क में है।

1728 में, अंग्रेजी खगोलशास्त्री जेम्स ब्रैडले ने तारकीय विपथनों को देखते हुए प्रकाश की गति की गणना की, जो कि सूर्य के चारों ओर पृथ्वी की गति के कारण स्थिति में उनका स्पष्ट परिवर्तन है। इस परिवर्तन के कोण को मापने और पृथ्वी की गति को घटाकर, जिसे वह उस समय ज्ञात डेटा से गणना कर सकता था, ब्रैडली बहुत अधिक सटीक संख्या के साथ आया था। उन्होंने निर्वात में प्रकाश की गति की गणना 301,000 किमी / घंटा की थी।

पानी में हवा की गति से प्रकाश की गति की तुलना करना

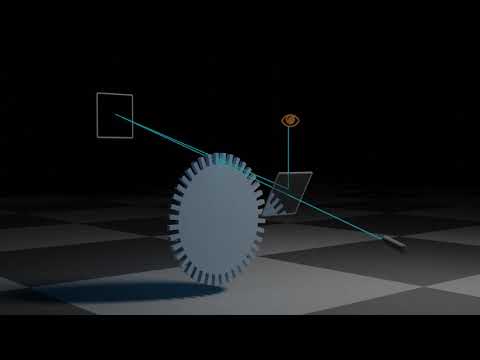
प्रकाश की गति को मापने के लिए अगला व्यक्ति फ्रांसीसी दार्शनिक आर्मंड हिप्पोलीटे फ़िज़ो था, और उसने खगोलीय टिप्पणियों पर भरोसा नहीं किया। इसके बजाय, उन्होंने एक बीम स्प्लिटर, एक घूर्णन दांतेदार पहिया और प्रकाश स्रोत से 8 किमी की दूरी पर रखा दर्पण से मिलकर एक उपकरण का निर्माण किया। वह पहिया के रोटेशन की गति को समायोजित कर सकता है ताकि प्रकाश की किरण दर्पण की ओर जा सके लेकिन वापसी किरण को अवरुद्ध कर सके। उसकी गणना सी, जो उन्होंने 1849 में प्रकाशित किया था, यह 315,000 किमी / सेकंड था, जो ब्रैडलिस की तरह सटीक नहीं था।

एक साल बाद, एक फ्रांसीसी भौतिक विज्ञानी, लियोन फौकॉल्ट, दांतेदार पहिया के लिए एक घूर्णन दर्पण को प्रतिस्थापित करके फ़िज़ियस प्रयोग में सुधार हुआ। सी के लिए Foucaults का मूल्य 298,000 किमी / घंटा था, जो अधिक सटीक था, और इस प्रक्रिया में, Foucault ने एक महत्वपूर्ण खोज की। घूर्णन दर्पण और स्थिर एक के बीच पानी की एक ट्यूब डालकर, उन्होंने निर्धारित किया कि हवा में प्रकाश की गति पानी की गति से अधिक है। यह इस बात के विपरीत था कि प्रकाश के कोरपसकुलर सिद्धांत ने भविष्यवाणी की थी और यह स्थापित करने में मदद की कि प्रकाश एक तरंग है।

1881 में, ए। ए। माइकलसन ने एक इंटरफेरोमीटर का निर्माण करके फॉक्सॉल्ट्स माप में सुधार किया, जो मूल बीम के चरणों की तुलना करने और वापस लौटने में सक्षम था और एक स्क्रीन पर एक हस्तक्षेप पैटर्न प्रदर्शित करता था। उसका परिणाम 299,853 किमी / सेकंड था।

मिशेलसन ने उपस्थिति की पहचान करने के लिए इंटरफेरोमीटर विकसित किया था ईथर, एक भूतिया पदार्थ जिसके माध्यम से प्रकाश तरंगों को फैलाने के लिए सोचा गया था। भौतिक विज्ञानी एडवर्ड मोरले के साथ किया गया उनका प्रयोग एक विफलता थी, और इसने आइंस्टीन को यह निष्कर्ष निकालने के लिए प्रेरित किया कि प्रकाश की गति एक सार्वभौमिक स्थिरांक है जो सभी संदर्भ फ्रेम में समान है। यही विशेष सापेक्षता सिद्धांत की नींव थी।

प्रकाश की गति के लिए समीकरण का उपयोग करना

1926 में खुद को सुधारने तक माइकलसन मूल्य को स्वीकार कर लिया गया था। तब से, कई शोधकर्ताओं द्वारा कई तकनीकों का उपयोग करके मूल्य को परिष्कृत किया गया है। ऐसी ही एक तकनीक कैविटी रेज़ोनरेटर विधि है, जो एक ऐसे उपकरण का उपयोग करती है जो विद्युत प्रवाह उत्पन्न करता है। यह एक मान्य विधि है क्योंकि 1800 के दशक के मध्य में मैक्सवेल के समीकरणों के प्रकाशन के बाद, भौतिकविदों ने सहमति व्यक्त की है कि प्रकाश और बिजली दोनों विद्युत चुम्बकीय तरंग घटनाएं हैं, और दोनों एक ही गति से यात्रा करते हैं।

वास्तव में, मैक्सवेल ने अपने समीकरणों को प्रकाशित करने के बाद, मुक्त स्थान की चुंबकीय पारगम्यता और विद्युत पारगम्यता की तुलना करके अप्रत्यक्ष रूप से सी को मापना संभव हो गया। दो शोधकर्ताओं, रोजा और डोरसी ने 1907 में ऐसा किया था और प्रकाश की गति की गणना 299,788 किमी / घंटा की थी।

1950 में, ब्रिटिश भौतिकविदों लुई एसेन और ए.सी. गॉर्डन-स्मिथ ने अपनी तरंगदैर्घ्य और आवृत्ति को मापकर प्रकाश की गति की गणना करने के लिए एक गुहा प्रतिध्वनि का उपयोग किया। प्रकाश की गति दूरी प्रकाश की यात्रा के बराबर है घ समय से विभाजित Δt: c = d / =t। विचार करें कि एकल तरंग दैर्ध्य के लिए समय λ एक बिंदु को पारित करने के लिए तरंग की अवधि है, जो आवृत्ति का पारस्परिक है v, और आपको प्रकाश सूत्र की गति मिलती है:

c = νλ

डिवाइस एसेन और गॉर्डन-स्मिथ का उपयोग एक के रूप में जाना जाता है गुहा प्रतिध्वनि तरंगमीटर। यह एक ज्ञात आवृत्ति का एक विद्युत प्रवाह उत्पन्न करता है, और वे तरंग के आयाम को मापकर तरंग दैर्ध्य की गणना करने में सक्षम थे। उनकी गणना में 299,792 किमी / सेकंड की पैदावार हुई, जो अब तक का सबसे सटीक निर्धारण था।

लेजर का उपयोग करके एक आधुनिक माप पद्धति

एक समकालीन माप तकनीक फ़िज़ियो और फौकॉल्ट द्वारा नियोजित बीम-विभाजन विधि को फिर से जीवित करती है, लेकिन सटीकता में सुधार करने के लिए लेजर का उपयोग करती है। इस विधि में, एक स्पंदित लेजर बीम विभाजित होता है। एक किरण एक डिटेक्टर के पास जाती है, जबकि दूसरा एक दर्पण से कुछ दूरी पर लंबवत यात्रा करता है। दर्पण बीम को एक दूसरे दर्पण पर वापस प्रतिबिंबित करता है जो इसे एक दूसरे डिटेक्टर को दर्शाता है। दोनों डिटेक्टरों को एक आस्टसीलस्कप तक झुका दिया जाता है, जो दालों की आवृत्ति को रिकॉर्ड करता है।

आस्टसीलस्कप दालों की चोटियों को अलग किया जाता है क्योंकि दूसरा बीम पहले वाले की तुलना में अधिक दूरी की यात्रा करता है। चोटियों के पृथक्करण और दर्पणों के बीच की दूरी को मापकर, प्रकाश किरण की गति को प्राप्त करना संभव है। यह एक सरल तकनीक है, और यह काफी सटीक परिणाम देता है। ऑस्ट्रेलिया में न्यू साउथ वेल्स विश्वविद्यालय के एक शोधकर्ता ने 300,000 किमी / सेकंड के मूल्य को दर्ज किया।

प्रकाश की गति को मापने से कोई लंबी अवधि नहीं बनती है

वैज्ञानिक समुदाय द्वारा उपयोग की जाने वाली मापने की छड़ी मीटर है। यह मूल रूप से भूमध्य रेखा से उत्तरी ध्रुव की दूरी के दस-दसवें हिस्से के रूप में परिभाषित किया गया था, और बाद में परिभाषा को क्रिप्टन -86 के उत्सर्जन लाइनों में से एक की तरंग दैर्ध्य की एक निश्चित संख्या के रूप में बदल दिया गया था। 1983 में, वजन और माप पर सामान्य परिषद ने उन परिभाषाओं को खत्म कर दिया और इसे अपनाया:

मीटर एक सेकंड में 1 / 299,792,458 में एक वैक्यूम में प्रकाश की किरण द्वारा तय की गई दूरी है, जहां दूसरा सीज़ियम -133 परमाणु के रेडियोधर्मी क्षय पर आधारित है।

प्रकाश की गति के मामले में मीटर को परिभाषित करना मूल रूप से 299,792,458 मीटर / सेकंड पर प्रकाश की गति को ठीक करता है। यदि एक प्रयोग एक अलग परिणाम देता है, तो इसका मतलब है कि उपकरण दोषपूर्ण है। प्रकाश की गति को मापने के लिए अधिक प्रयोग करने के बजाय, वैज्ञानिक अपने उपकरणों को जांचने के लिए प्रकाश की गति का उपयोग करते हैं।

प्रायोगिक उपकरण को शांत करने के लिए प्रकाश की गति का उपयोग करना

प्रकाश की गति भौतिकी में विभिन्न प्रकार के विपक्ष में दिखाई देती है, और इसकी तकनीकी रूप से अन्य मापा आंकड़ों से गणना करना संभव है। उदाहरण के लिए, प्लैंक ने प्रदर्शित किया कि एक क्वांटम की ऊर्जा, जैसे कि एक फोटॉन, प्लांक स्थिरांक (h) की आवृत्ति के बराबर है, जो 6.6262 x 10 के बराबर है^-34 Joule⋅second। चूंकि आवृत्ति है c / λ, प्लैंक समीकरण को तरंग दैर्ध्य के संदर्भ में लिखा जा सकता है:

ई = एचपीओ = एचसी / λ

सी = ईओएन / एच

एक ज्ञात तरंग दैर्ध्य के प्रकाश के साथ एक फोटोइलेक्ट्रिक प्लेट पर बमबारी करके और उत्सर्जित इलेक्ट्रॉनों की ऊर्जा को मापना, इसके लिए एक मूल्य प्राप्त करना संभव है सी। प्रकाश कैलकुलेटर की इस प्रकार की गति को मापने के लिए आवश्यक नहीं है, हालांकि, क्योंकि सी है परिभाषित यह क्या है हालांकि, इसका उपयोग तंत्र का परीक्षण करने के लिए किया जा सकता है। अगर Eλ / एच सी होने के लिए बाहर नहीं आता है, कुछ गलत है या तो इलेक्ट्रॉन ऊर्जा के माप या घटना प्रकाश की तरंग दैर्ध्य के साथ।

एक वैक्यूम में प्रकाश की गति एक सार्वभौमिक निरंतर है

यह एक वैक्यूम में प्रकाश की गति के संदर्भ में मीटर को परिभाषित करने के लिए समझ में आता है, क्योंकि यह ब्रह्मांड में सबसे मौलिक स्थिरांक है। आइंस्टीन ने दिखाया कि यह गति की परवाह किए बिना हर संदर्भ बिंदु के लिए समान है, और इसकी सबसे तेज चीज भी ब्रह्मांड में यात्रा कर सकती है - कम से कम, द्रव्यमान के साथ कुछ भी। आइंस्टीन समीकरण, और भौतिकी में सबसे प्रसिद्ध समीकरण में से एक, ई = एमसी², सुराग प्रदान करता है कि ऐसा क्यों है।

अपने सबसे पहचानने योग्य रूप में, आइंस्टीन समीकरण केवल बाकी निकायों पर लागू होता है। हालाँकि, सामान्य समीकरण में शामिल है लोरेंत्ज़ कारक γ, कहाँ पे √ = 1 / √ (1- वी²/सी²)। एक द्रव्यमान के साथ गति में एक शरीर के लिए म और वेग v, आइंस्टीन समीकरण लिखा जाना चाहिए ई = एमसी²γ। जब आप इसे देखते हैं, तो आप देख सकते हैं कि कब v = 0, γ = 1 और आपको मिलता है ई = एम सी².

हालाँकि, जब v = c, γ अनंत हो जाता है, और आपको जो निष्कर्ष निकालना है, वह यह है कि यह किसी भी परिमित द्रव्यमान को गति देने के लिए ऊर्जा की अनंत मात्रा लेगा। इसे देखने का एक अन्य तरीका यह है कि द्रव्यमान प्रकाश की गति से अनंत हो जाता है।

मीटर की वर्तमान परिभाषा प्रकाश की गति को दूरी के स्थलीय माप के लिए मानक बनाती है, लेकिन इसका उपयोग लंबे समय से अंतरिक्ष में दूरी मापने के लिए किया जाता है। एक प्रकाश वर्ष वह दूरी है जो प्रकाश एक सांसारिक वर्ष में यात्रा करता है, जो 9.46 × 10 निकलता है¹⁵ म।

यह कई मीटर को समझने के लिए बहुत अधिक है, लेकिन एक प्रकाश वर्ष को समझना आसान है, और क्योंकि प्रकाश की गति सभी जड़त्वीय संदर्भ फ्रेम में स्थिर है, इसकी एक विश्वसनीय इकाई है। इसकी वर्ष के आधार पर थोड़ा कम विश्वसनीय था, जो कि एक समय सीमा है जो किसी अलग ग्रह से किसी के लिए कोई प्रासंगिकता नहीं होगी।