कैसे एक वक्र की ढलान की गणना करने के लिए

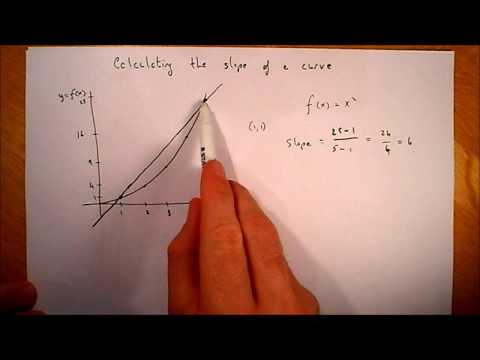
एक वक्र की ढलान की गणना करने के लिए, आपको घटता फ़ंक्शन के व्युत्पन्न की गणना करने की आवश्यकता है। व्युत्पन्न वक्र पर बिंदु की रेखा स्पर्शरेखा के ढलान का समीकरण है जिसकी ढलान की आप गणना करना चाहते हैं। यह कर्व्स समीकरण की सीमा है क्योंकि यह इंगित बिंदु तक पहुंचता है। व्युत्पन्न की गणना के लिए कई विधियां हैं, लेकिन शक्ति नियम सबसे सरल विधि है और इसका उपयोग सबसे बुनियादी बहुपद समीकरणों के लिए किया जा सकता है।

वक्र का समीकरण लिखिए। इस उदाहरण के लिए, समीकरण 3X ^ 2 + 4X + 6 = 0 का उपयोग किया जाएगा।

मूल समीकरण में किसी भी स्थिरांक को पार करें। एक ढलान परिवर्तन की एक दर है, और क्योंकि स्थिरांक नहीं बदलते हैं, उनकी ढलान 0 के बराबर होती है, और इसलिए वे व्युत्पन्न में मौजूद नहीं होंगे।

प्रत्येक एक्स शब्द की शक्ति को गुणक के रूप में शब्द के सामने लाएं, और नई शक्ति प्राप्त करने के लिए मूल शक्ति से एक को घटाएं। तो, उदाहरण से 3X ^ 2 2 (3X ^ 1), या 6X हो जाता है, और 4X 4 हो जाता है। ये दो चरण पावर नियम की मूल बातें हैं। नमूना व्युत्पन्न समीकरण अब 6X + 4 = 0 पढ़ता है।

मूल वक्र के बिंदु को चुनें, जिसकी ढलान की आप गणना करना चाहते हैं, और ढलान मान प्राप्त करने के लिए X को व्युत्पन्न समीकरण में समन्वयित करें। उदाहरण में, बिंदु पर ढलान (1,16) 10 होगी।