विषय
- इलेक्ट्रिक फील्ड्स, समझाया गया
- गुरुत्वाकर्षण और विद्युत क्षेत्रों के बीच संबंध
- विद्युत संभावित ऊर्जा समीकरण
- दो आरोपों के बीच विद्युत क्षमता
- इलेक्ट्रिक पोटेंशियल एनर्जी उदाहरण
जब आप पहली बार विद्युत क्षेत्रों में कणों की गति का अध्ययन करते हैं, तो इस बात की ठोस संभावना होती है कि आपने पहले से ही गुरुत्वाकर्षण और गुरुत्वाकर्षण क्षेत्रों के बारे में कुछ सीखा है।
जैसा कि होता है, द्रव्यमान के साथ कणों को नियंत्रित करने वाले कई महत्वपूर्ण संबंध और समीकरण इलेक्ट्रोस्टैटिक इंटरैक्शन की दुनिया में समकक्ष हैं, जो एक चिकनी संक्रमण के लिए बनाते हैं।
आपने शायद निरंतर द्रव्यमान और वेग के एक कण की ऊर्जा को सीखा है v का योग है गतिज ऊर्जा इक, जो संबंध का उपयोग करते हुए पाया जाता है mv2/ 2, और गुरुत्वाकर्षण स्थितिज ऊर्जा इपी, उत्पाद का उपयोग कर पाया MGH कहाँ पे जी त्वरण गुरुत्वाकर्षण के कारण है और ज ऊर्ध्वाधर दूरी है।
जैसा कि आप देखते हैं, एक आवेशित कण की विद्युत संभावित ऊर्जा को खोजने में कुछ अनुरूप गणित शामिल होता है।
इलेक्ट्रिक फील्ड्स, समझाया गया
एक आवेशित कण क्यू एक विद्युत क्षेत्र स्थापित करता है इ कि कण से सभी दिशाओं में सममित रूप से बाहर की ओर विकिरण लाइनों की एक श्रृंखला के रूप में कल्पना की जा सकती है। यह क्षेत्र एक बल प्रदान करता है एफ अन्य आवेशित कणों पर क्ष। बल की परिमाण Coulombs स्थिर द्वारा शासित है क और आरोपों के बीच की दूरी:
F = frac {kQq} {r ^ 2}
क का परिमाण है 9 × 109 एन एम2/ सी2, कहाँ पे सी भौतिकी में आवेश की मूल इकाई, कोलम्ब के लिए है। याद रखें कि धनात्मक रूप से आवेशित कण ऋणात्मक रूप से आवेशित कणों को आकर्षित करते हैं जबकि आवेशों को पीछे हटाते हैं।
आप देख सकते हैं कि बल व्युत्क्रम के साथ घटता है वर्ग बढ़ती दूरी, न केवल "दूरी के साथ," जिस स्थिति में आर कोई घातांक नहीं होगा।
बल भी लिखा जा सकता है एफ = QE, या वैकल्पिक रूप से, विद्युत क्षेत्र के रूप में व्यक्त किया जा सकता है इ = एफ/क्ष.
गुरुत्वाकर्षण और विद्युत क्षेत्रों के बीच संबंध
द्रव्यमान के साथ एक विशाल वस्तु जैसे कि तारा या ग्रह म एक गुरुत्वाकर्षण क्षेत्र स्थापित करता है जिसे विद्युत क्षेत्र के समान ही कल्पना की जा सकती है। यह क्षेत्र एक बल प्रदान करता है एफ द्रव्यमान के साथ अन्य वस्तुओं पर म एक तरह से जो दूरी के वर्ग के साथ परिमाण में घट जाती है आर उनके बीच:
F = frac {GMm} {r ^ 2}
कहाँ पे जी सार्वभौमिक गुरुत्वाकर्षण स्थिरांक है।
इन समीकरणों और पिछले अनुभाग में उन लोगों के बीच सादृश्य स्पष्ट है।
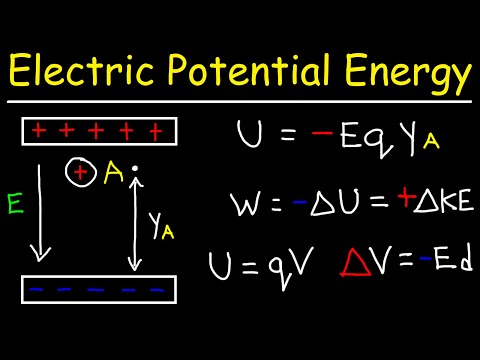
विद्युत संभावित ऊर्जा समीकरण
इलेक्ट्रोस्टैटिक संभावित ऊर्जा का सूत्र, लिखित यू आवेशित कणों के लिए, आवेशों के परिमाण और ध्रुवता और उनके पृथक्करण दोनों के लिए खाते:
U = frac {kQq} {r}यदि आप उस कार्य को याद करते हैं (जिसमें ऊर्जा की इकाइयाँ हैं) बल दूरी है, तो यह बताता है कि यह समीकरण बल समीकरण से भिन्न क्यों है "आर"हर में। पूर्व को दूरी से गुणा करना आर उत्तरार्द्ध देता है।
दो आरोपों के बीच विद्युत क्षमता
इस बिंदु पर आप सोच रहे होंगे कि शुल्क और विद्युत क्षेत्र की इतनी चर्चा क्यों हुई है, लेकिन वोल्टेज का कोई उल्लेख नहीं है। यह मात्रा, वीहै, बस प्रति यूनिट चार्ज बिजली की संभावित ऊर्जा है।
विद्युत संभावित अंतर उस कार्य का प्रतिनिधित्व करता है जो एक कण को स्थानांतरित करने के लिए विद्युत क्षेत्र के खिलाफ किया जाना चाहिए क्ष क्षेत्र द्वारा निहित दिशा के खिलाफ। वह है, अगर इ एक धनात्मक आवेशित कण द्वारा उत्पन्न होता है क्यू, वी एक सकारात्मक रूप से आवेशित कण को स्थानांतरित करने के लिए प्रति इकाई आवेश में आवश्यक कार्य है आर उनके बीच, और एक समान आवेश परिमाण के साथ ऋणात्मक रूप से आवेशित कण को स्थानांतरित करने के लिए भी आर दूर से क्यू.
इलेक्ट्रिक पोटेंशियल एनर्जी उदाहरण
एक कण क्ष +4.0 नैनोकोलम्ब के चार्ज के साथ (1 एनसी = 10 –9 Coulombs) की दूरी है आर = 50 सेंटीमीटर (यानी 0.5 मीटर) -8.0 एनसी के प्रभार से दूर। इसकी संभावित ऊर्जा क्या है?
start {align} U & = frac {kQq} {r} & = frac {(9 × 10 ^ 9 ; {N} ; {m} ^ 2 / {C} ^ 2; ) × (+8.0 × 10 ^ {- 9} ;; {{C}) × (-4.0 × 10 ^ {- 9} _! {{C})} {0.5 ; {m}} & = 5.76 × 10 ^ {- 7} ; {J} end {संरेखित}नकारात्मक संकेत आरोपों के विपरीत होने का परिणाम है और इसलिए एक दूसरे को आकर्षित करते हैं। संभावित ऊर्जा में दिए गए बदलाव के परिणामस्वरूप जितना काम किया जाना चाहिए उतना ही परिमाण लेकिन विपरीत दिशा है, और इस मामले में आरोपों को अलग करने के लिए सकारात्मक काम किया जाना चाहिए (बहुत कुछ गुरुत्वाकर्षण के खिलाफ एक वस्तु उठाने की तरह)।