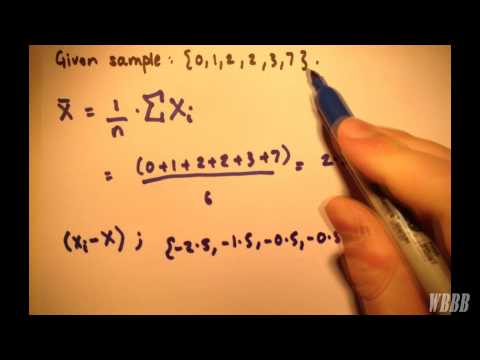
विषय
- चरण 1: नमूना माध्य की गणना करें
- चरण 2: अलग-अलग मूल्यों से मतलब घटाना
- चरण 3: व्यक्तिगत भिन्नताओं को स्क्वायर करें
- चरण 4: विचलन के वर्गों को जोड़ें
- बोनस दौर
जैसे अवधारणाओं मतलब तथा विचलन क्या आटा, टमाटर सॉस और मोज़ेरेला चीज़ पिज्जा के लिए हैं: सिद्धांत रूप में सरल हैं, लेकिन इस तरह के परस्पर संबंध रखने वाले अनुप्रयोगों की इतनी विविधता है कि बुनियादी शब्दावली का ट्रैक खोना आसान है और जिस क्रम में आपको कुछ ऑपरेशन करने होंगे।
नमूने के माध्यम से वर्ग विचलन की राशि की गणना दो महत्वपूर्ण वर्णनात्मक आंकड़ों की गणना करने के तरीके के साथ एक कदम है: विचरण और मानक विचलन।
चरण 1: नमूना माध्य की गणना करें
एक माध्य (अक्सर एक औसत के रूप में संदर्भित) की गणना करने के लिए, अपने नमूने के व्यक्तिगत मूल्यों को एक साथ जोड़ें और एन द्वारा विभाजित करें, आपके नमूने में कुल आइटम। उदाहरण के लिए, यदि आपके नमूने में पाँच क्विज़ स्कोर शामिल हैं और व्यक्तिगत मान 63, 89, 78, 95 और 90 हैं, तो इन पाँच मूल्यों का योग 415 है, और इसीलिए इसका अर्थ 415 = 5 = 83 है।
चरण 2: अलग-अलग मूल्यों से मतलब घटाना
वर्तमान उदाहरण में, माध्य 83 है, इसलिए इस घटाव के अभ्यास से (63-83) = -20 (89-83) = 6, (78-83) = -5, (95-83) = 12 का मान प्राप्त होता है , और (90-83) = 7. इन मूल्यों को विचलन कहा जाता है, क्योंकि वे इस बात का वर्णन करते हैं कि प्रत्येक मूल्य नमूने से किस हद तक विचलित होता है।
चरण 3: व्यक्तिगत भिन्नताओं को स्क्वायर करें
इस स्थिति में, स्क्वरिंग -20 में 400, स्क्वेरिंग 6 में 36, स्क्वेरिंग -5 में 25, स्क्वेरिंग में 12 में 144, और स्क्वेरिंग में 7 में 49 अंक दिए गए हैं। ये मूल्य हैं, जैसा कि आप उम्मीद करेंगे, पूर्व में निर्धारित विचलन के वर्ग कदम।
चरण 4: विचलन के वर्गों को जोड़ें
औसत से विचलन के वर्गों का योग प्राप्त करने के लिए, और इस तरह व्यायाम पूरा करें, आपके द्वारा चरण 3 में गणना किए गए मान जोड़ें। इस उदाहरण में, यह मान 400 + 36 + 25 + 144 + 49 = 654 है। योग विचलन के वर्गों को अक्सर सांख्यिकी प्रतिमान में SSD के रूप में संक्षिप्त किया जाता है।
बोनस दौर
यह अभ्यास एक नमूने के विचरण की गणना में शामिल कार्य का थोक करता है, जो कि n-1 द्वारा विभाजित SSD है, और नमूने के मानक विचलन, जो कि विचरण का वर्गमूल है।