
ऑटोक्रॉलेशन एक सांख्यिकीय विधि है जिसका उपयोग समय श्रृंखला विश्लेषण के लिए किया जाता है। उद्देश्य अलग-अलग समय के चरणों में एक ही डेटा में दो मूल्यों के सहसंबंध को मापना है। यद्यपि समय डेटा का उपयोग आटोक्लेरलेशन की गणना करने के लिए नहीं किया जाता है, सार्थक परिणाम प्राप्त करने के लिए आपकी समय वृद्धि समान होनी चाहिए। स्वावलंबी गुणांक दो उद्देश्यों को पूरा करता है। यह डेटा सेट में गैर-यादृच्छिकता का पता लगा सकता है। यदि डेटा सेट में मान यादृच्छिक नहीं हैं, तो ऑटोकॉर्पेशन विश्लेषक को एक उपयुक्त समय श्रृंखला मॉडल चुनने में मदद कर सकता है।
जिस डेटा का आप विश्लेषण कर रहे हैं, उसके लिए औसत या औसत की गणना करें। माध्य डेटा मानों की संख्या (n) द्वारा विभाजित सभी डेटा मानों का योग है।
अपनी गणना के लिए एक समय अंतराल (के) पर निर्णय लें। लैग वैल्यू एक पूर्णांक है जो यह दर्शाता है कि कितने समय में एक मान को दूसरे से अलग करता है। उदाहरण के लिए, (y1, t1) और (y6, t6) के बीच अंतराल पांच है, क्योंकि दोनों मानों के बीच 6 - 1 = 5 समय के चरण हैं। यादृच्छिकता के लिए परीक्षण करते समय, आप आमतौर पर केवल लैग k = 1 का उपयोग करते हुए एक ऑटोकॉर्लेशन गुणांक की गणना करेंगे, हालांकि अन्य लैग मान भी काम करेंगे। जब आप एक उपयुक्त समय श्रृंखला मॉडल का निर्धारण कर रहे हैं, तो आपको प्रत्येक के लिए एक अलग अंतराल मान का उपयोग करते हुए, ऑटोकैरेलेशन मूल्यों की एक श्रृंखला की गणना करने की आवश्यकता होगी।
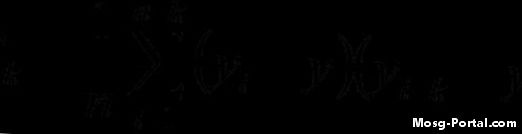
दिए गए फॉर्मूले का उपयोग करके ऑटोकॉवेरियन फ़ंक्शन की गणना करें। उदाहरण के लिए, क्या आप lag k = 7 का उपयोग करके तीसरी पुनरावृत्ति (i = 3) की गणना कर रहे हैं, फिर उस पुनरावृत्ति की गणना इस तरह दिखाई देगी: (y3 - y-bar) (y10 - y-bar) Iterate "i" के मान और फिर योग लेते हैं और इसे डेटा सेट में मानों की संख्या से विभाजित करते हैं।
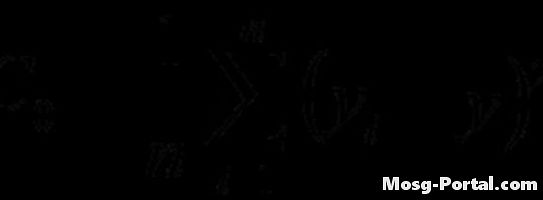
दिए गए सूत्र का उपयोग करके विचरण फ़ंक्शन की गणना करें। गणना autocovariance फ़ंक्शन के समान है, लेकिन लैग का उपयोग नहीं किया जाता है।

स्वतःभरण गुणांक प्राप्त करने के लिए विचरण समारोह द्वारा ऑटोकॉवेरियन फ़ंक्शन को विभाजित करें। आप दिखाए गए अनुसार दो कार्यों के लिए सूत्रों को विभाजित करके इस चरण को बायपास कर सकते हैं, लेकिन कई बार, आपको अन्य उद्देश्यों के लिए ऑटोकोविरियन और विचरण की आवश्यकता होगी, इसलिए उन्हें व्यक्तिगत रूप से भी गणना करना व्यावहारिक है।