विषय
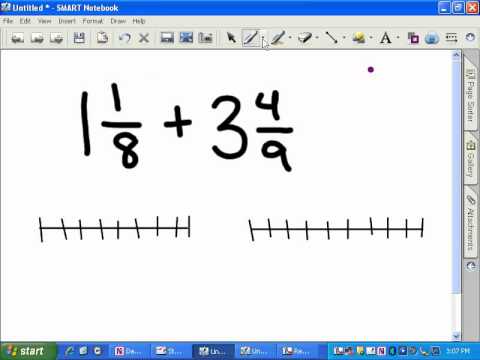
गणित में एक बेंचमार्क एक सहज ज्ञान युक्त उपकरण है जो किसी समस्या को हल करने में मदद करता है। वे सबसे अधिक अंश और दशमलव समस्याओं के साथ उपयोग किए जाते हैं। छात्रों को पेपर या कैलकुलेटर के अंशों को परिवर्तित करने या कम करने के लिए जोड़ और घटाव समस्याओं को हल करने के लिए बेंचमार्क का उपयोग करना आसान हो सकता है।
अनुमान
एक बेंचमार्क एक छात्र को सामान्य संख्या को एक अंश या दशमलव संख्या का अनुमान लगाने में मदद करता है। उदाहरण के लिए, एक छात्र जल्दी से सीख सकता है कि अंश 1/2 का मतलब आधा, 0.50 या 50 प्रतिशत अंतर्ज्ञान के कारण है। हालाँकि, अब जब छात्र इस प्रक्रिया को जानता है, तो छात्र अनुमान लगा सकता है कि कोई संख्या 1/2 से अधिक है या छोटी। उदाहरण के लिए, 1/4 (0.25 या 25 प्रतिशत) को सहज रूप से 1/2 से कम माना जा सकता है, लेकिन 3/4 (0.75 या 75 प्रतिशत) अधिक है।
पूरे संबंध
अंश केवल रिश्तों का एक हिस्सा अपने पूरे करने के लिए कर रहे हैं। उदाहरण के लिए, 1/2 एक संपूर्ण इकाई का 50 प्रतिशत या 0.50 है। इस बिंदु पर बच्चों को पढ़ाने की कोशिश करने के लिए, कई बेंचमार्क अभ्यास उनके आरोही क्रम में अंशों को सूचीबद्ध करने पर आधारित होते हैं। 1. खंड 2/5, 1/3, 2/3, और 3/4 को बेंचमार्क का उपयोग करके आरोही क्रम में रखा जा सकता है। अंतर्ज्ञान से पता चलता है कि 1/3 लगभग 1 का 33 प्रतिशत है, जबकि 3/4 का 75 प्रतिशत है। अंश 2/5 1/5 से एक अधिक है, जो 20 गुना 5 गुना 1 के बराबर 20 प्रतिशत है, जिसका अर्थ 2 / है। 5 40 प्रतिशत या 0.40 है। अंत में, 2/3 1/3 से अधिक है, इसलिए इसे 66 प्रतिशत होना चाहिए। भिन्नों के बढ़ते क्रम में 1/3 (0.33), 2/5 (0.40), 2/3 (0.66), और 3/4 (0.75) होते हैं, ये सभी 1 नंबर तक होते हैं।
0, 1/2, 1
गणित के शिक्षक अपने छात्रों को सूचित करेंगे कि उनकी गणित की समस्याओं में उपयोग करने के लिए सबसे अच्छे बेंचमार्क 0, 1/2 और 1 हैं। इन नंबरों के साथ, एक छात्र अपने सिर में गणना करने की कोशिश कर सकता है कि प्रत्येक नंबर के करीब या दशमलव क्या हैं। एक उदाहरण 0.1 की तुलना में दशमलव 0.01 हो सकता है। बेंचमार्क संख्याओं का उपयोग करते हुए, एक छात्र जान सकता है कि 0.01 0 से 0 के करीब है और इसलिए 0.1 बड़ी संख्या है। एक घटाव समस्या में, छात्र यह पता लगा सकते हैं कि समीकरण 0.1 - 0.01 = 0.99, सबसे अधिक संभावना सही है क्योंकि .99 लगभग 1 है।
त्वरित अनुमान
दशमलव में भी भिन्नता को बदलने के बिना, कुछ अंश समस्याओं को हल करने का सबसे तेज़ तरीका उन्हें 0, 1/2 और 1 से जोड़ना है। उदाहरण के लिए, यदि कोई छात्र मुड़ने के बजाय 7/8 + 11/12 जैसी समस्या प्राप्त करता है। दशमलव और आकलन में भिन्नता, छात्र सहजता से जान सकता है कि इनमें से हर एक अंश कम है कि 1. क्योंकि 7/8 और 11/12 परिभाषा के अनुसार, प्रत्येक 1 से कम हैं। इसलिए, समाधान अधिक नहीं हो सकता है 2 की तुलना में। हालांकि यह तुरंत जवाब नहीं देता है, यह त्वरित अनुमान बेंचमार्क एक छात्र को यह जानने में मदद करता है कि पैमाने पर उत्तर आम तौर पर कहां होना चाहिए।